[33v] 52^a. Linea data in plano ad unum punctum terminata, invenire in plano coni sectionem vocatam parabolen, cuius diameter¹ data linea, sum[S:45]mitas terminus lineae: quae autem a sectione ducitur ad diametrum in dato angulo, possit contentum rectangulum sub recepta sub ipsa ad summitatem sectioni, et² sub altera quadam data linea.

Sit positione data linea ab terminata ad a. // gd autem magnitudine. // Angulusque datus primum³ rectus.

// Oportet invenire in subiecto plano parabolen: cuius diameter sit ab. // Summitas a. // Recta⁴ dg. // Et ordinate ductae ad rectum angulum applicatae⁵.

// Sit ipsius gd 1/4 gh⁶. // Et producta ba sit ae maior, quam gh⁷. // Et ipsarum gd ea⁸ media proportionalis⁹ t per 9^am 6ⁱ Euclidis.

// Eritque per 17^am 6ⁱ¹⁰ gd ea sicut t ea.

// Sed gd minor, quam¹¹ quadrupla ipsius ea ergo et t minus, quam quadruplum¹² ipsius ea.

// Quare et ipsa t minor, quam dupla ipsius ea. Et ideo possibile est per 22^am primi Euclidis ex ipsa t geminisque ea triangulum constituere.

// Constituatur itaque aez in quo ae ez aequales: et ze aequalis ipsi t rectum ad subiectum planum.

// Et agatur zc quidem ipsi ae atque ac ipsi ze aequidistantes.

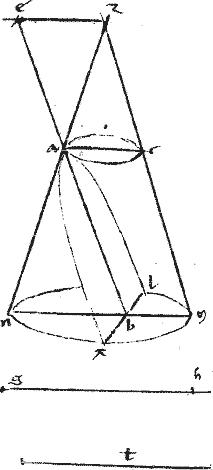
// Et intelligatur conus: cuius vertex z basis autem circa diametrum ac circulus rectus ad planum acz eritque talis conus rectus, quandoquidem az zc aequalia.

// Cuius conica superficies indefinita.

// Et secetur conus plano, quod parallelum sit circulo ca. // Sitque sectio in conica superficie, per 4^am huius, circulus mxn rectus ad planum mzn existente communi sectione linea mn.

// Sitque subiecti plani et circuli communis sectio xl.

// Et quoniam tam subiectum planum, quam circulus rectus est ad mzn. // Ideo, per 19^am 11ⁱ Euclidis xl communis eorum sectio recta erit ad mzn.

// Quare xl et omnis eius parallelus recta erit ad ab et bn.

// Cumque ab diameter parallelus sit ipsi zc. Iam, per 11^am huius, sectio, quam facit subiectum planum in cono, parabole est: cuius quidem diameter ab vertex a et [A:34r] ordinate ductae ad rectos diametro.

// Et, quoniam gd t ea sunt in proportione continua: atque ipsae t ez¹³ ac aequales: itemque ipsae ea az zc aequales. Ideo gd ac az sunt in proportione continua.

// Quare per 17^am 6ⁱ¹⁴ Euclidis ac azc sicut¹⁵ gd ¹⁶ az.

// Et ideo, per 11^am huius, gd recta diameter¹⁷ est factae xal parabolae¹⁸.

// Factum ergo¹⁹, quod proponitur faciendum.

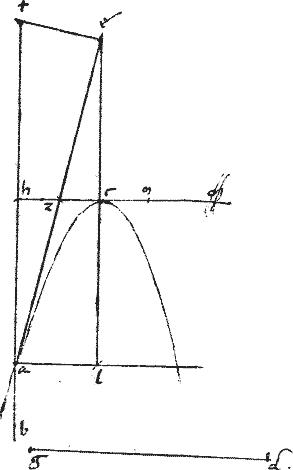
// Et lcm²⁵ aequale sit ^to al.

// Quibus peractis, describatur parabole, cuius diameter sit cl. Summitas c. // Recta cm. // Et ordinate ductae ad rectos diametro, ut dudum docuimus: quae sit ac. // Ibit enim talis parabola per a quoniam al potest lcm. // Et per 33^am huius ae tanget sectionem quandoquidem lc aequalis²⁶ ce.

// Cumque ta aequidistet ipsi cl²⁷ erit, per 46^am huius, ipsa tab²⁸ diameter sectionis: bifariam enim²⁹ secabit actas in sectione penes ae tangentem et ad angulum tae ordinate ductas ad ipsam tab diametrum. // Et quoniam ate azh sunt similia: ideo per 4^am 6ⁱ Euclidis ta ea sicut³⁰ za ah. // Quare³¹ dupla ipsius ta duplam ipsius ae sicut za ah.

// Ergo per 49^am huius, gd recta diameter est, sectionis ac paraboles videlicet factae.

// Rursus igitur factum³², quod proponebatur faciendum.