39^a Si hyperbolen, vel ellipsim, vel circuli periferiam linea tangens coincidat diametro: et a tactu applicetur linea ad diametrum ordinate: sumaturque utravis duarum linearum, quarum haec quidem est inter applicatam et centrum sectionis: illa vero inter applicatam et tangentem: habebit ad sumptam¹ applicata compositam rationem ex ea, quam² reliqua duarum linearum³ ad applicatam, et ex ea, quam rectum⁴ speciei latus ad⁵ transversum.

Sit hyperbole, ellipsis,

// Dico iam quod ratio ge ed componitur ex duabus rationibus videlicet rectae transversam ze eg .

Item quod ratio ge ez componitur ex [[duabus]]6 videlicet rectae transversam de eg .

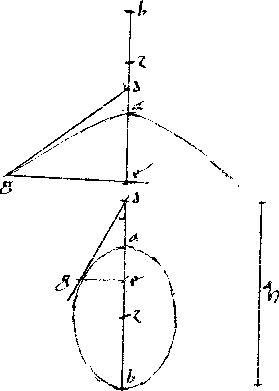
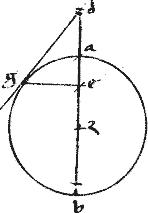
// Sit enim ipsi

zed aequale egh. // Et quoniam per antepremissam zed ge sicut transversa ad rectam. // Ideo erit et egh ge hoc est h ge sicut transversa ad rectam, et conversim.

// Et quoniam zed egh aequalia⁷ ideo per 15^am 6ⁱ Euclidis ez eg sicut⁸ h ed.

// Sed ratio ge ed componitur ex rationibus ge h h ed

fuitque ge h sicut recta transversam: et h ed sicut ez eg.

// Igitur ratio ge ed componitur ex rationibus rectae transversam ze eg .

[A:22v] // Similiter pro ratione ge ed [[sumentes]] rationem ge ez demonstrabimus,

quod ratio ge ez componitur ex rationibus rectae transversam ed eg .

// Quemadmodum proponitur demonstrandum.