12^a Si conus plano secetur per axim, secetur autem et altero plano secante basim coni per rectam ad rectos existentem basi trianguli per axim: et diameter sectionis producta coincidat uni laterum tri[A:7r]anguli per axim extra coni verticem; quae a sectione ducta est aequidistans communi sectioni secantis plani et basis coni usque ad diametrum sectionis, poterit id, quod superficies adiacens ad quamdam lineam, ad quam rationem habet¹ linea in rectum manens diametro sectionis occurrensque exterius lateri trianguli, quam² quadratum, quod sit a ducta a summitate coni penes diametrum sectionis in basim trianguli ad contentum sub basis segmentis a ducta³ factis, et latitudinem habens receptam sub ipsa a⁴ diametro ad verticem sectionis, excedens specie, simili et similiter iacente, contento sub coincidente lateri trianguli, et sub illa, ad quam possunt ductae. Vocetur autem haec sectio hyperbole.

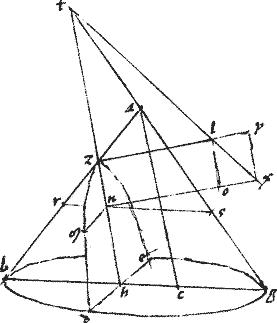
[S:14] Conus, cuius vertex a basisque circulus bg secetur plano per axim: sitque sectio per 3^am5 abg secetur et altero plano secante basim coni per rectam de ad rectos ipsi bg⁶ et faciente in conica superficie sectionem dze cuius diameter zh⁷ coincidat uni laterum, quod sit ga apud t. // Item ac penes zh. // Et zl ad rectos ipsi zh ita ut tz zl sit sicut ac bcg. // Et a contingenti puncto sectionis, utpote m ducatur mn penes de. // Et connexa tl compleatur zlon. // Et collapsis in unum tl no apud x compleatur lpxo.

Dico iam quod⁸ mn⁹ potest zx adiacens scilicet ad ipsam zl sub latitudine zn et excedens specie lx simili ^lo tzl. Nam, ducta primum rns penes bg iam per 24^am 6ⁱ¹⁰ Euclidis ratio ca bcg componitur

ex rationibus ac cg bc

Et propter similitudinem triangulorum¹¹ et proportionem laterum eadem ratio componetur ex rationibus th¹² hg atque zh hb¹³ et similiter eadem componetur ex rationibus tn ns atque zn nr.

Verum, per 24^am14 predictam ratio tnz snr componitur ex rationibus tn ns // zn nr.

Igitur tnz snr erit sicut quadratum ca ¹⁵ bcg et ideo sicut tz zl ac sicut tn nx propter   similitudinem¹⁶.

[A:7v] Verum per primam sexti tn nx sicut¹⁷ tnz znx.

Igitur tnz znx erit sicut tnz snr.

Quare, per 9^am 5ⁱ snr aequale znx.

Cumque per 15^am 11ⁱ planum, in quo mn rs aequedistet plano circuli bgd quae basis est coni.

Ideo per 4^am huius puncta rms erunt in periferia circuli, cuius diameter rs.

Ergo per 8^am 6ⁱ¹⁸ Euclidis snr aequum erit mn quare et mn aequum ^lo znx.

Quod erat demonstrandum.

Vocetur autem talis sectio hyperbole: ipsa autem hz¹⁹ ad quam possunt ductae ad zh ordinatae: voceturque eadem et recta: transversa autem zt: ipsum autem tzl species sectionis.

om. :

Et manifestum est, quod sicut tz zl sic est tnz ad znx hoc est ad mn namque eadem ratio fuit, quae tn nx.