2a Si in utravis superficierum secundum verticem positarum, duo puncta ponantur, et recta puncta connectens non eat per verticem, cadit1 intra superficiem: ulterius vero producta2 cadet extra.
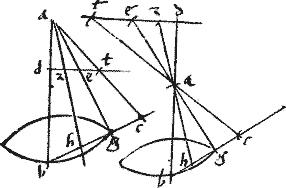
In conica superficie, cuius vertex a circulus, per quem fertur linea describens bg3 capiantur duo puncta d e ita ut recta de non cadat super a punctum.
Dico quod de recta4 est intra superficiem5: et protracta cadit extra.
Ducantur enim, ad ae6 rectae: quae per praecedentem erunt in ipsa superficie: et connexa bg iampridem totum planum trianguli abg intra superficiem cadit: quandoquidem omnes rectae a vertice a ductae ad quaevis puncta ipsius rectae bg demptis extremis, cadunt per praemissae corollarium, intra7 superficiem. Unde punctum quodvis in ipsa de ut pote z cadit intra superficiem: nam recta [A:2v] az producta cadet ad aliquod punctum basis bg utpote ad punctum h estque8 per praemissae corollarium ah intra superficiem: et perinde punctum z intra superficiem: et similiter omnia puncta rectae de ostendentur cadere intra superficiem, demptis extremis. Producta autem de ad extra utpote9 ad punctum t cadet extra superficiem. Nam connexa at occurret ipsi bg extra productae ut puta ad c: quare per corollarium praemissum tota recta atc cadet extra superficiem et perinde punctum t et omne aliud punctum10 ipsius de extra productae cadet extra superficiem. Quod ostendisse oportuit.