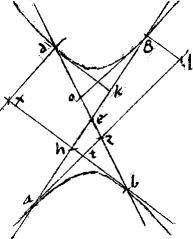
1 [A:67v] 8^a Iisdem subiectis, per ipsa puncta g, d apud quae diametri coincidunt sectionibus ducantur aequidistantes tangentibus, et iisdem alternatim concurrentes ipsae dx, gl.

Dico iam quod ¹ dh, gz sunt aequalia: quodque ² xk, ol similiter aequalia sunt ad invicem. 2 Cum enim per primam huius aht, tbz sint invicem aequalia. // Et ideo ahb, azb aequalia. // Iam per 39^am primi Euclidis lineae coniunctae ab, hz aequidi[S:90]stantes sunt. // Quare, per 2^am 6ⁱ Euclidis ea ah sicut³ eb bz. // Sed ga ae sicut db be utraque enim utriusque dupla. // Ex aequo igitur est sicut ga ah sicut db bz. // Verum dupla rationis ga ah est quae^{4 li} gal hat similia enim sunt triangula propter aequidistantiam linearum. 3 // Dupla quoque rationis db bz est quae^{5 li} dbx zbt. // Ergo sicut dbx zbt sic gal hat⁶ et permutatim sicut dbx gal sic zbt hat. // Fuit autem zbt equum hat. // Igitur et dbx aequum⁷ gal. // Quare et residua ⁸ dt, tg aequalia. // Et communi ablato et ⁹ rursum et reliqua ¹⁰ dh, gz aequalia. // 4 Quibus apponantur dke, goe. Iam per primam huius, vel per additam 33^ae primi Conicorum invicem aequalia. Et constabuntur ¹¹ xk, ol aequalia. Sicut proponitur demonstrandum.