|
7a Iisdem subiectis, si in utraque sectionum puncta quaedam relicta sint: et ab ipsis aequidistantes ducantur tangentibus coincidentes tangentibus et diametris; tunc quadrilatera centro sectionum punctisque relictis interiecta a ductis ad diametros facta aequalia sunt. 1 Item quadrilatera illorum partialia a tangentibus ad diametros assumpta aequalia sunt. Demum duo reliqua quadrilatera a centro ad reliquos tangentium con[A:67r]cursus, a tangentibus extrorsum hinc inde ad diametros recepta aequalia sunt. Unde et ex aequalibus tetragonis conflata non secus aequalia erunt ad invicem.
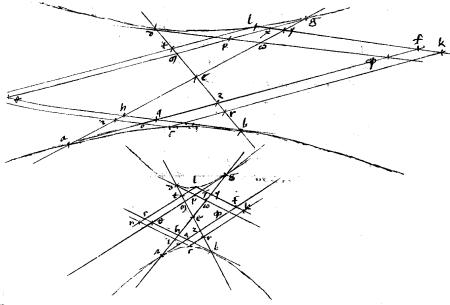 2 Sint contrapositae, quarum diametri aeg, deb. // Centrum e. // Relicta puncta c, l. // Tangentes sectionem ab sint aoqz
2 Sint contrapositae, quarum diametri aeg, deb. // Centrum e. // Relicta puncta c, l. // Tangentes sectionem ab sint aoqz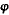 f, bqh f, bqh s // Tangentes sectionem gd sint gxpm s // Tangentes sectionem gd sint gxpm 1, dp 1, dp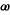 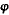 . // Quae quidem singulae illis singulis sunt per additam 43ae primi aequidistantes. // A relictis autem punctis c, l tangentibus aequidistantes sint crk, coin. 3 // Itemque ltsn, lyfk2. // Dico iam quod . // Quae quidem singulae illis singulis sunt per additam 43ae primi aequidistantes. // A relictis autem punctis c, l tangentibus aequidistantes sint crk, coin. 3 // Itemque ltsn, lyfk2. // Dico iam quod   3 el, ec sunt aequalia. // Itemque 3 el, ec sunt aequalia. // Itemque   4 eq, ep aequalia. // Denique quod 4 eq, ep aequalia. // Denique quod   5 e 5 e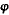 , e , e aequalia sunt ad invicem. // Namque, per 2am huius aequalia sunt ad invicem. // Namque, per 2am huius  aio aequale est aio aequale est  ro6 or. // Positoque communi ro6 or. // Positoque communi  7 eo fiet totum 7 eo fiet totum  aez toti aez toti  8 ec aequale. // 4 Similiter arguendo 8 ec aequale. // 4 Similiter arguendo  gem aequale iam9 gem aequale iam9  10 el. // Verum 10 el. // Verum   aez, gem per additam 43ae primi Conicorum sunt aequalia. // Igitur et ipsa aez, gem per additam 43ae primi Conicorum sunt aequalia. // Igitur et ipsa   11 el, lc12 sunt aequalia. // Igitur cum 11 el, lc12 sunt aequalia. // Igitur cum   ahq, g ahq, g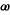 p propter aequidistantiam linearum sint aequiangula13 et per additam 33ae primi Conicorum, ipsae ah, g p propter aequidistantiam linearum sint aequiangula13 et per additam 33ae primi Conicorum, ipsae ah, g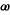 14 sint aequales: erunt et ad invicem aequilatera et aequalia. 5 // Fuerunt autem et 14 sint aequales: erunt et ad invicem aequilatera et aequalia. 5 // Fuerunt autem et   aez, gem aequalia. // Supersunt ergo ipsa aez, gem aequalia. // Supersunt ergo ipsa   15 eq, ep aequalia. // Denique quoniam aq, gp aequales: et in parallelogrammo pq ipsae q, 15 eq, ep aequalia. // Denique quoniam aq, gp aequales: et in parallelogrammo pq ipsae q, 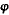 , p , p aequales. Ideo totae a, aequales. Ideo totae a, 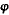 , g , g aequales. // Quare, propter aequidistantiam linearum, aequales. // Quare, propter aequidistantiam linearum,   a a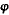 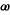 , g , g h aequalia. // A quibus auferantur h aequalia. // A quibus auferantur   la aez, gem iampridem aequalia. 6 // Et supererunt la aez, gem iampridem aequalia. 6 // Et supererunt   16 e 16 e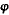 , e , e aequalia. // Unde sequitur ut et aequalia. // Unde sequitur ut et   17 tc, li sint aequalia. Item ut 17 tc, li sint aequalia. Item ut   18 mq, 18 mq, 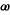  sint aequalia. // Et similiter bina quaevis ex binis aequalibus confecta. // Quod erat demostrandum. sint aequalia. // Et similiter bina quaevis ex binis aequalibus confecta. // Quod erat demostrandum.
|
