[A:53r] 142 Superest nunc ostendere nonnulla, quae dudum nos ostensurum promisimus.
1a
143 Horum primum est, quod cubus sive quadrata columna cum quadrato et triangulo collateralibus coniuncta facit triplum suae quadratae pyramidis.
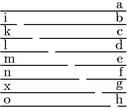
144 Ut si ponatur numeri abcdefgh quorum h sit unitas, g binarius, f ternarius et sic deinceps per unitatis crementum usque ad a maximum. Deinde ipsis bcdefgh resarciantur excessus singuli singulis, quibus scilicet singuli ab ipso a maximo exceduntur. Hoc est ipsi b apponatur i unitas; ipsi c ipse k binarius; et caeteri lmnxo51 caeteris per unitatis crementum successive52 augmentati. Sic ib kc ld me nf xg oh singuli fient ipsi a aequales.

145
Iam ergo, quoniam quot sunt unitates in a numero totidem sunt numeri a bi ck dl em fn gx ho. Iam horum ![]() ti simul conficiunt cubum, cuius latus est a. Et quoniam hgfedcba53 ab ipsam h unitate et per unitatis crementum crescunt, ideo ipsorum congeries, quae iam fit ex h unitate in ipsorum hgfedcba congeriem, est triangulus, cuius latus ipse numerus a. Item
ti simul conficiunt cubum, cuius latus est a. Et quoniam hgfedcba53 ab ipsam h unitate et per unitatis crementum crescunt, ideo ipsorum congeries, quae iam fit ex h unitate in ipsorum hgfedcba congeriem, est triangulus, cuius latus ipse numerus a. Item ![]() ti numeri ipsorum abcdefgh conficiunt pyramidem quadratam, cuius basis est
ti numeri ipsorum abcdefgh conficiunt pyramidem quadratam, cuius basis est ![]() ipsius a. Licet ergo hic consyderare quatuor54 species collaterales numerorum, scilicet cubum quod est aggregatum ipsorum a bi ck dl em fn gx ho, quadratum ipsius a, triangulum, quod est aggregatum ipsorum abcdefgh, nec non pyramidem quadratam, quod est aggregatum ex
ipsius a. Licet ergo hic consyderare quatuor54 species collaterales numerorum, scilicet cubum quod est aggregatum ipsorum a bi ck dl em fn gx ho, quadratum ipsius a, triangulum, quod est aggregatum ipsorum abcdefgh, nec non pyramidem quadratam, quod est aggregatum ex ![]()
![]() tis ipsorum abcdefgh cuius basis est
tis ipsorum abcdefgh cuius basis est ![]() ipsius a. Quae quatuor numerorum species procreantur ex latere a et ideo collaterales vocantur: quem [A:53v] admodum ex earum diffinitionibus constat, et per tabellam superius expositam apparet. Demonstrandum igitur est, quod cubus, quadratus et triangulus praedicti simul coniuncti semper conficiunt triplum pyramidis quadratae praedictae: hoc est, quod aggregatum ex
ipsius a. Quae quatuor numerorum species procreantur ex latere a et ideo collaterales vocantur: quem [A:53v] admodum ex earum diffinitionibus constat, et per tabellam superius expositam apparet. Demonstrandum igitur est, quod cubus, quadratus et triangulus praedicti simul coniuncti semper conficiunt triplum pyramidis quadratae praedictae: hoc est, quod aggregatum ex ![]()
![]() a ib kc ld me nf xg oh cum
a ib kc ld me nf xg oh cum ![]() to ipsius a et cum aggregato ipsorum abcdefgh simul facit semper triplum aggregati ex ipsis
to ipsius a et cum aggregato ipsorum abcdefgh simul facit semper triplum aggregati ex ipsis ![]()
![]() tis ipsorum abcdefgh, hoc est quod
tis ipsorum abcdefgh, hoc est quod
|
147 Quae demonstratio sic procedit.
148 In primis per 4am secundi Elementorum Euclidis
|
150
Apponatur ergo utrobique ![]()
![]() a cum
a cum ![]() h in totum abcdefgh. Eritque
h in totum abcdefgh. Eritque
|
|
155 Superest ergo demonstrare quod
|
157 Quod sic demonstrabitur. Nam
|
|
161
Dicta vero 7 ![]() la sub h dictisque multiplicibus una cum
la sub h dictisque multiplicibus una cum ![]() sub h dictoque aggregato aequalia sunt his scilicet
sub h dictoque aggregato aequalia sunt his scilicet ![]() bi
bi ![]() kc
kc ![]() ld
ld ![]() me
me ![]() nf
nf ![]() xg
xg ![]() oh una cum
oh una cum ![]() h et aggregati ex abcdefgh.
h et aggregati ex abcdefgh.
162 Quandoquidem
|
165 Praemissa demonstratio desumpta est ex 10a propositione Archimedis de Spiralibus.

2
166 Praeterea, si quis multiplicet aggregatum ex proposito quopiam numero et unitate in aggregatum ex quadrato numeri propositi et ex dimidio eiusdem propositi: conficiet ex tali multiplicatione triplum aggregati quadratorum ab [A:55v] unitate usque ad quadratum propositi numeri inclusive: hoc est triplum quadratae pyramidis proposito numero collateralis.
167
Quod sic ostendam. In58 praemissa descriptione sit propositus numerus a. Aio quod aggregatum ex ah multiplicatum in congeriem ex quadrato ipsius a dimidioque eiusdem a producit triplum pyramidis59 ![]() tae collateralis. Namque cum a ductus in
tae collateralis. Namque cum a ductus in ![]() a faciat cubum ipsius a, iam ah totus in
a faciat cubum ipsius a, iam ah totus in ![]() tum a faciet aggregatum ex cubo et quadrato talibus. Cumque per regulam progressionis ha totus in dimidium ipsius a faciat aggregatum ipsorum abcdefgh hoc est triangulum collateralem ipsius a. Propterea et ha totus in aggregatum ex
tum a faciet aggregatum ex cubo et quadrato talibus. Cumque per regulam progressionis ha totus in dimidium ipsius a faciat aggregatum ipsorum abcdefgh hoc est triangulum collateralem ipsius a. Propterea et ha totus in aggregatum ex ![]() to a dimidioque eiusdem a producet aggregatum ex cubo, quadrato, et triangulo praedictis: fuit autem, per praecedentem, id aggregatum triplum pyramidis quadratae praedictae. Igitur ah totus multiplicatus in aggregatum ex ipsius a
to a dimidioque eiusdem a producet aggregatum ex cubo, quadrato, et triangulo praedictis: fuit autem, per praecedentem, id aggregatum triplum pyramidis quadratae praedictae. Igitur ah totus multiplicatus in aggregatum ex ipsius a ![]() et ex eiusdem a dimidio producit triplum pyramidis praedictae collateralis, hoc est triplum cumuli ex
et ex eiusdem a dimidio producit triplum pyramidis praedictae collateralis, hoc est triplum cumuli ex ![]()
![]() tis abcdefgh numerorum coniunctis confecti. Et hoc fuit demonstrandum.
tis abcdefgh numerorum coniunctis confecti. Et hoc fuit demonstrandum.

[A:56r] 3
168 Nunc ostendam quod columna pentagona una cum duplo quadrati collateralis semper efficit triplum suae pyramidis pentagonae.
169
Namque numerus pentagonus constat ex ![]() to et immediate praecedenti triangulo. Et similiter pyramis pentagona conflatur ex pyramide quadrata et pyramide triangula immediate praecedenti. Item columna pentagona constat ex columna quadrata seu cubo collaterali60 et ex columna triangula et
to et immediate praecedenti triangulo. Et similiter pyramis pentagona conflatur ex pyramide quadrata et pyramide triangula immediate praecedenti. Item columna pentagona constat ex columna quadrata seu cubo collaterali60 et ex columna triangula et ![]() lo immediate praecedentibus. Cumque columna quadrata seu cubus cum
lo immediate praecedentibus. Cumque columna quadrata seu cubus cum ![]() to et
to et ![]() lo collateralibus una faciat triplum suae pyramidis quadratae (per antepraemissam), itemque columna triangula cum duplo trianguli collateralis coniuncta efficiat triplum suae pyramidis
lo collateralibus una faciat triplum suae pyramidis quadratae (per antepraemissam), itemque columna triangula cum duplo trianguli collateralis coniuncta efficiat triplum suae pyramidis ![]() lae, ut alibi ostensum est. Atque ideo columna illa, triangula61 quae unum secum
lae, ut alibi ostensum est. Atque ideo columna illa, triangula61 quae unum secum ![]() lum assumpserat ad constructionem columnae pentagonae, hic unum tantum, sibi postulet
lum assumpserat ad constructionem columnae pentagonae, hic unum tantum, sibi postulet ![]() lum ad consummandum triplum suae pyramidis. Qui quidem
lum ad consummandum triplum suae pyramidis. Qui quidem ![]() lus iunctus cum
lus iunctus cum ![]() lo sequenti, (62 quem scilicet sibi cubus assumpserat cum
lo sequenti, (62 quem scilicet sibi cubus assumpserat cum ![]() to ad integrandum triplum suae pyramidis
to ad integrandum triplum suae pyramidis ![]() tae) conficiat
tae) conficiat ![]() tum aequalem dicto; propterea sequitur, ut columna pentagona cum duplo quadrati collateralis coniuncta semper faciat triplum suae pyramidis collateralis: sicut proponitur demonstrandum.
tum aequalem dicto; propterea sequitur, ut columna pentagona cum duplo quadrati collateralis coniuncta semper faciat triplum suae pyramidis collateralis: sicut proponitur demonstrandum.
|
|
172
Igitur columna pentagona 17566 cum duplo ![]() ti 25, hoc est cum 50, facit triplum pyramidis pentagonae 75.
ti 25, hoc est cum 50, facit triplum pyramidis pentagonae 75.
173 Quod erat demonstrandum.
4
174
Subiungemus et illud, quod demonstrandum simul promiseramus, quod columna hexagona prima cum collateralis quadrati duplo et cum praecedenti ![]() lo iuncta, facit triplum hexagonae suae pyramidis.
lo iuncta, facit triplum hexagonae suae pyramidis.
175
Nam numerus hexagonus primus constat ex pentagono collaterali et ![]() lo praecedenti. Et similiter pyramis hexagona prima constat ex pyramide pentagona collaterali et pyramide
lo praecedenti. Et similiter pyramis hexagona prima constat ex pyramide pentagona collaterali et pyramide ![]() la praecedenti. Item columna hexagona prima conflatur ex columna pentagona collaterali et ex columna
la praecedenti. Item columna hexagona prima conflatur ex columna pentagona collaterali et ex columna ![]() la cum
la cum ![]() lo praecedentibus. Cumque per praecedentem, columna pentagona cum duplo
lo praecedentibus. Cumque per praecedentem, columna pentagona cum duplo ![]() ti collateralis faciat triplum suae pyramidis
ti collateralis faciat triplum suae pyramidis ![]() nae, columna vero
nae, columna vero ![]() la, ut alibi ostensum est, cum duplo sui
la, ut alibi ostensum est, cum duplo sui ![]() li efficiat triplum suae pyramidis: propterea semper necesse est, ut columna hexagona praedicta cum duplo
li efficiat triplum suae pyramidis: propterea semper necesse est, ut columna hexagona praedicta cum duplo ![]() ti praedicti et uno
ti praedicti et uno ![]() lo (nam alium
lo (nam alium ![]() lum assumpserat sibi columna
lum assumpserat sibi columna ![]() la ad construendam columnam
la ad construendam columnam ![]() nam) coniuncta perficiat triplum suae pyramidis hexagonae sicut proponitur demonstrandum.
nam) coniuncta perficiat triplum suae pyramidis hexagonae sicut proponitur demonstrandum.
|
177
Igitur et
178
columna ![]() 22574 cum
22574 cum ![]()
![]() 25 2575 et
25 2575 et ![]() lo 1076 faciet triplum pyramidis
lo 1076 faciet triplum pyramidis ![]() ae 9577.
ae 9577.
179 Quod erat demonstrandum.
5
180
Hinc sequitur ut eadem columna hexagona prima cum suo hexagono et collaterali ![]() lo coniuncta faciat idem triplum suae pyramidis.
lo coniuncta faciat idem triplum suae pyramidis.
181
Namque cum ipse hexagonus constet ex collaterali ![]() to binisque praecedentibus
to binisque praecedentibus ![]()
![]() is, atque
is, atque ![]()
![]() lorum horum unus cum
lorum horum unus cum ![]() lo collaterali memorato conficiat dictum
lo collaterali memorato conficiat dictum ![]() tum. Iam dictus hexagonus una78 cum collaterali dicto
tum. Iam dictus hexagonus una78 cum collaterali dicto ![]() lo aequabit aggregatum ex dicti
lo aequabit aggregatum ex dicti ![]() ti duplo dictorumque praece [A:57r] dentium
ti duplo dictorumque praece [A:57r] dentium ![]()
![]() lorum uno: sed, per praecedentem, columna hexagona, de qua loquimur, una cum dicti
lorum uno: sed, per praecedentem, columna hexagona, de qua loquimur, una cum dicti ![]() ti duplo, ac dictorum triangulorum uno coniuncta conflabat triplum suae pyramidis. Igitur et eadem hexagona columna cum dicto suo hexagono, dictoque collaterali
ti duplo, ac dictorum triangulorum uno coniuncta conflabat triplum suae pyramidis. Igitur et eadem hexagona columna cum dicto suo hexagono, dictoque collaterali ![]() lo simul posita non minus, integrabit dictum memoratae pyramidis suae triplum, quod erat ostendendum.
lo simul posita non minus, integrabit dictum memoratae pyramidis suae triplum, quod erat ostendendum.
| ||||||||||||
183 Hinc constat aperte propositum.
6
184 Columnam vero triangulam semper esse collaterali pentagonae pyramidi aequalem haud difficulter demonstrare possumus.
185
Exponatur ab unitate numeri quotcumque et per unitatem crescentes ordinatim scilicet a unitas, bc binarius, de ternarius, fg quaternarius et deinceps eodem ordine quotlibet: et ex ipsis bc de fg procreentur eorum quadrati. Et unitates ghkl faciant altitudinem postremi quadrati. Item super quadratos bc de fg applicentur ![]() li praecedentes: hoc est
li praecedentes: hoc est ![]() to bc unitas m79:
to bc unitas m79: ![]() to de ternarius n, quadrato fg senarius o et deinceps alii sequentibus. Iam enim ex diffinitione bc
to de ternarius n, quadrato fg senarius o et deinceps alii sequentibus. Iam enim ex diffinitione bc ![]() tus cum m unitate facit pentagonum ab unitate 2um, bc
tus cum m unitate facit pentagonum ab unitate 2um, bc ![]() tus cum n
tus cum n ![]() lo pentagonum sequentem, fg
lo pentagonum sequentem, fg ![]() tus cum o
tus cum o ![]() lo pentagonum sequentem et deinceps, alii alios.
lo pentagonum sequentem et deinceps, alii alios.
186
Et sicut a est ipse m quia uterque unitas, ita n constat ex aggregato a bc; triangulus autem o ex aggregato a bc de; triangulus quoque sequens in ordine, ex [A:57v] aggregato ipsorum a bc de fg. Unde ex diffinitione ex multitudine horum numerorum, in postremum ![]() lum producitur columna
lum producitur columna ![]() la, hoc est in hoc exemplo, ex quaternario (cum quatuor sint numeri pentagoni expositi) in aggregatum ipsorum a bc de, fg80 quod est
la, hoc est in hoc exemplo, ex quaternario (cum quatuor sint numeri pentagoni expositi) in aggregatum ipsorum a bc de, fg80 quod est ![]() lus quaternario collateralis, fiet columna
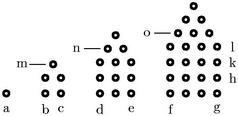
lus quaternario collateralis, fiet columna ![]() la; et ex aggregatione unitatis et trium sequentium pentagonorum construetur pyramis pentagona dictae columnae collateralis. Demonstrandum ergo est quod productum ex quaternario in totum a bc de fg aequale est aggregato unitatis et trium sequentium pentagonorum.
la; et ex aggregatione unitatis et trium sequentium pentagonorum construetur pyramis pentagona dictae columnae collateralis. Demonstrandum ergo est quod productum ex quaternario in totum a bc de fg aequale est aggregato unitatis et trium sequentium pentagonorum.
Hoc modo m unitas transposita super a unitatem faciet binarium: qui cum ![]() to bc constituet planum numerum sub latitudine binarii et longitudine ternarii facientis 2um
to bc constituet planum numerum sub latitudine binarii et longitudine ternarii facientis 2um ![]() lum ab unitate. Deinde n ternarius transpositus super dicti plani longitudinem augebit celsitudinem dicti plani ad aequalitatem
lum ab unitate. Deinde n ternarius transpositus super dicti plani longitudinem augebit celsitudinem dicti plani ad aequalitatem ![]() ti de cum quo planum constituet sub latitudine ternarii et longitudine senarii, qui sequentem
ti de cum quo planum constituet sub latitudine ternarii et longitudine senarii, qui sequentem ![]() lum facit. Postremo o senarius transpositus super longitudinem dictam sibi parem, augendo plani celsitudinem ad aequalitatem
lum facit. Postremo o senarius transpositus super longitudinem dictam sibi parem, augendo plani celsitudinem ad aequalitatem ![]() ti fg cum ipso
ti fg cum ipso ![]() to planum conficiet sub latitudine quaternarii et longitudine denarii, quod est aggregatum ex a bc de fg. Quam ob rem productum ex quaternario, quod est multitudo assumptorum numerorum, in totum81aggregatum ex a bc de fg, hoc est in
to planum conficiet sub latitudine quaternarii et longitudine denarii, quod est aggregatum ex a bc de fg. Quam ob rem productum ex quaternario, quod est multitudo assumptorum numerorum, in totum81aggregatum ex a bc de fg, hoc est in ![]() lum collateralem quod est 10, consumat congeriem ex unitate, sequentibus tribus pentagonis compositam: et similiter in quotcumque numeris ab unitate ordinatis faciemus, semper concludetur82 columnam triangulam esse aequalem collaterali pentagonae pyramidi sicut demon [A:58r] strandum proponitur.
lum collateralem quod est 10, consumat congeriem ex unitate, sequentibus tribus pentagonis compositam: et similiter in quotcumque numeris ab unitate ordinatis faciemus, semper concludetur82 columnam triangulam esse aequalem collaterali pentagonae pyramidi sicut demon [A:58r] strandum proponitur.
7a
187 Si propositi cuiuspiam numeri et83 numeri unitate maioris congeries multiplicetur in planum ab eisdem contentum: numerus ex multiplicatione productus erit sexcuplus ad aggregatum quadratorum ab unitate usque ad quadratum propositi numeri inclusive ordinatorum.
188
Esto propositus quicumque numerus a et numerus b unitate maior: quorum congeries c, planus vero sub ipsis ab contentus sit d. Et ex c in ipsum d fiat e. Dico quod e numerus sexcuplus est ad aggregatum ![]()
![]() torum ab unitate inclusive usque ad
torum ab unitate inclusive usque ad ![]() tum ipsius a ordinatorum. Cum enim ex a in b fiat d iam per diffinitionem multiplicationis, erit sicut b
tum ipsius a ordinatorum. Cum enim ex a in b fiat d iam per diffinitionem multiplicationis, erit sicut b ![]() unitatem sic utique d
unitatem sic utique d ![]() a. Sit itaque a duplus ipsius f. Atque g aggregatum ex
a. Sit itaque a duplus ipsius f. Atque g aggregatum ex ![]() to a et ex f. Sic enim d erit aggregatum ipsarum gf. Item sit h duplus ipsius b. Eritque ex aequa proportione, sicut h
to a et ex f. Sic enim d erit aggregatum ipsarum gf. Item sit h duplus ipsius b. Eritque ex aequa proportione, sicut h ![]() unitatem, sic utique d
unitatem, sic utique d ![]() f. Et eversim, sicut h
f. Et eversim, sicut h ![]() c sic d
c sic d ![]() g. Sit ergo k84 planus ex g in h. Eritque per 15am sexti Euclidis k85 planus aequalis plano e qui sub cd continetur. Sed, ut ostensum fuit in 2a harum propositionum, ex b, quod est aggregatum ex a proposito numero et ex unitate, in g, quod fuit aggregatum ex
g. Sit ergo k84 planus ex g in h. Eritque per 15am sexti Euclidis k85 planus aequalis plano e qui sub cd continetur. Sed, ut ostensum fuit in 2a harum propositionum, ex b, quod est aggregatum ex a proposito numero et ex unitate, in g, quod fuit aggregatum ex ![]() ipsius a et ex f eius dimidio, producitur triplum aggregati quadratorum ab unitate inclusive usque ad
ipsius a et ex f eius dimidio, producitur triplum aggregati quadratorum ab unitate inclusive usque ad ![]() tum ipsius a, igitur ex h duplo ipsius b in g producetur sexcuplum praedicti quadratorum aggregati. Sexcuplus itaque erit k ad praedictum aggregatum quadratorum. Aequalis autem fuit ipsi k plano ipse e planus: et e igitur sexcuplus erit ad non semel dictum quadratorum aggregatum.
tum ipsius a, igitur ex h duplo ipsius b in g producetur sexcuplum praedicti quadratorum aggregati. Sexcuplus itaque erit k ad praedictum aggregatum quadratorum. Aequalis autem fuit ipsi k plano ipse e planus: et e igitur sexcuplus erit ad non semel dictum quadratorum aggregatum.
189 Quod fuit demonstrandum.

190 Catanae kalendas decembris 1553.
8
191 Tres numeri trianguli in ordine triangulorum immediate sumpti, atque coniuncti efficiunt triplum medii cum unitate iunctum.
192 Patet facillime, nam differentia, qua postremus trium talium triangulorum excedit86 secundum est unitate maior, quam differentia, qua secundus87 excedit primum. Et ideo aggregatum ex primo et postremo facit duplum secundi cum unitate. Unde et aggregatum ex tribus simul faciet triplum secundi cum unitate: sicut proponitur.
9
193
Omnis triangulus duplicatus et cum duobus praecedente et sequente ![]() lis88 coniunctus facit quadruplum sui cum unitate.
lis88 coniunctus facit quadruplum sui cum unitate.
194 Sequitur ex praecedenti apertissime.
10
195
Omnis triangulus duplicatus cum duobus praecedente et sequente ![]() lis coniunctus facit aggregatum duorum quadratorum collateralium medio et maximo ex dictis
lis coniunctus facit aggregatum duorum quadratorum collateralium medio et maximo ex dictis ![]() lis89.
lis89.
196
Patet, nam ut ostendit Iordanus, duo collaterali et sequente90 trianguli faciunt quadratum maiori ![]() lo collateralem.
lo collateralem.
11
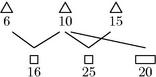
197
Omnis triangulus duplicatus cum duobus praecedente et sequente ![]() lis coniunctus, facit duplum parte altera longioris maximo ex dictis
lis coniunctus, facit duplum parte altera longioris maximo ex dictis ![]() lis collateralis cum91 unitate iunctum.
lis collateralis cum91 unitate iunctum.
198
Nam cum ex antepraemissa, dictum duplum medii ![]() li cum
li cum ![]() lis praecedente et sequente faciat quadruplum medii cum unitate: duplum autem medii constituat92 ipsum iam memoratum parte altera longiorem, ut ostendit Iordanus, sequitur iam apertissime id, quod proponitur.
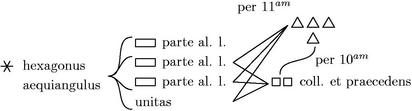
lis praecedente et sequente faciat quadruplum medii cum unitate: duplum autem medii constituat92 ipsum iam memoratum parte altera longiorem, ut ostendit Iordanus, sequitur iam apertissime id, quod proponitur.
|
[A:59r] 12
200 Hexagonus aequilaterus conflatur ex aggregatione parte altera longioris95 et quadrati collateralium una cum quadrato immediate praecedenti.
201
Nam per praecedentem, duplum ![]() li medii cum aggregato praecedentis et sequentis triangulorum facit duplum parte altera longioris maximo
li medii cum aggregato praecedentis et sequentis triangulorum facit duplum parte altera longioris maximo ![]() lo collateralis cum unitate iunctum. Per antepraemissam autem, facit aggregatum duorum quadratorum medio et maximo
lo collateralis cum unitate iunctum. Per antepraemissam autem, facit aggregatum duorum quadratorum medio et maximo ![]() lo collateralium: igitur aggregatum horum duorum
lo collateralium: igitur aggregatum horum duorum ![]()
![]() torum aequale erit aggregato ex dicto duplo96 parte altera longioris et unitate. Apponatur utrobique parte altera longior praedicto aequalis. Eritque aggregatum ex dictis duobus quadratis et ex parte altera longiore aequale triplo parte altera longioris cum unitate. Verum, ut antea demonstravimus in his arithmeticis, triplum huiusmodi parte altera longioris cum unitate iunctum facit hexagonum aequilaterum collateralem. Ergo et ipse hexagonus aequilaterus aequalis erit97 aggregato dictorum duorum quadratorum et dicti parte altera longioris. Sicut demonstrandum proponitur.
torum aequale erit aggregato ex dicto duplo96 parte altera longioris et unitate. Apponatur utrobique parte altera longior praedicto aequalis. Eritque aggregatum ex dictis duobus quadratis et ex parte altera longiore aequale triplo parte altera longioris cum unitate. Verum, ut antea demonstravimus in his arithmeticis, triplum huiusmodi parte altera longioris cum unitate iunctum facit hexagonum aequilaterum collateralem. Ergo et ipse hexagonus aequilaterus aequalis erit97 aggregato dictorum duorum quadratorum et dicti parte altera longioris. Sicut demonstrandum proponitur.
|
13
203 Si fuerint quotcumque numeri ab unitate, et per unitatem crescentes: productus ex postremo in aggregatum ex postremo et unitate duplus erit ad omnium crescentium congeriem.
204 Patet [A:59v] quoniam ex tali multiplicatione, per diffinitionem fit numerus parte altera longior proxime sequens. Hic autem per demonstrata Iordani, duplus est ad triangulum suum praecedentem, hoc est ad congeriem propositorum crescentium numerorum. Constat ergo propositum.
14a
205
Columna triangula cum duplo sui trianguli coniuncta triplum facit collateralis ![]() lae pyramidis.
lae pyramidis.
206
Hoc est, columna ![]() la, cuius celsitudo excedit binario celsitudinem suae pyramidis, est ad ipsam pyramidem tripla. Esto a unitas, b binarius, c ternarius, d quaternarius, e quinarius, f senarius, g septenarius, itaque deinceps ad libitum. Unde, cum a sit unitas, erit, per diffinitionem ab alter ab unitate
la, cuius celsitudo excedit binario celsitudinem suae pyramidis, est ad ipsam pyramidem tripla. Esto a unitas, b binarius, c ternarius, d quaternarius, e quinarius, f senarius, g septenarius, itaque deinceps ad libitum. Unde, cum a sit unitas, erit, per diffinitionem ab alter ab unitate ![]() lus. Et abc sequens
lus. Et abc sequens ![]() lus. Et abcd quartus
lus. Et abcd quartus ![]() lus. Et abcde quintus
lus. Et abcde quintus ![]() lus. Et sic successive. Esto igitur l postremus ex his quinque in proposito
lus. Et sic successive. Esto igitur l postremus ex his quinque in proposito ![]()
![]() lis. Numerus autem g unitate maior, quam f. Et ideo binario maior, quam e. Atque ex g in ipsum l fiat p. Demonstrandum est quod p quae iam est columna
lis. Numerus autem g unitate maior, quam f. Et ideo binario maior, quam e. Atque ex g in ipsum l fiat p. Demonstrandum est quod p quae iam est columna ![]() la, cuius basis
la, cuius basis ![]() lus l, binario excelsior pyramide
lus l, binario excelsior pyramide ![]() la, quam consummant quinque
la, quam consummant quinque ![]()
![]() li98 lhfca cuius basis est idem
li98 lhfca cuius basis est idem ![]() lus l, tripla est eiusdem pyramidis.
lus l, tripla est eiusdem pyramidis.
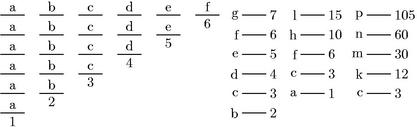
207
Erunt enim numeri gfedcb singuli [A:60r] aggregata duorum extremorum, hoc est unitatis et postremi constituentium singulos ![]() los qui sunt lhfca. Utpote g aggregatum ex af. Et f aggregatum ex ae. Et e aggregatum ex ad. Et d aggregatum ex ac. Et c aggregatum ex ab. Itaque ex f in h fiat n. Item ex e in f fiat m. Item ex d in c fiat k. Atque ex c in a fiat ipse c quoniam a est unitas.
los qui sunt lhfca. Utpote g aggregatum ex af. Et f aggregatum ex ae. Et e aggregatum ex ad. Et d aggregatum ex ac. Et c aggregatum ex ab. Itaque ex f in h fiat n. Item ex e in f fiat m. Item ex d in c fiat k. Atque ex c in a fiat ipse c quoniam a est unitas.
208
Ostendamque quod ipse p excedit99 ipsum n in triplo ipsius l. Sic. Per praecedentem, ex f qui aggregatur ex a unitate et ex extremo ipsorum abcde ducto in ipsum extremum e (qui est differentia ipsorum hl per diffinitionem ![]()
![]() lorum) producit duplum aggregati ex ipsis abcde, hoc est ipsius l qui
lorum) producit duplum aggregati ex ipsis abcde, hoc est ipsius l qui ![]() lus est, ex dictis abcde aggregatus. Igitur in tali duplo ipsius l, numerus qui fit ex f in l excedit ipsum n productum iam ex f in h. Verum, qui fit ex g in l scilicet ipse p excedit eum, qui ex f in l, in ipso numero l quandoquidem fg differunt unitate. Ergo, qui fit ex g in l scilicet p excedit ipsum n qui ex f in h, in triplo ipsius l. Eodemque processu ostendam, quod excessus n quo superat ipsum m triplus erit ipsius h quodque excessus m super k triplus erit ipsius f quodque excessus ipsius k super c triplus erit ipsius c. Nam c quia ternarius, triplus tandem per se constat esse ad a unitatem. Et perinde ipse p qui constat ex aggregatione dictorum quatuor excessum et ex c triplus erit [A:60v] ad aggregatum ex ipsis lhfca. Et similiter procedemus in quotcumque propositis numeris eodem processu dispositis. Quod erat demonstrandum.
lus est, ex dictis abcde aggregatus. Igitur in tali duplo ipsius l, numerus qui fit ex f in l excedit ipsum n productum iam ex f in h. Verum, qui fit ex g in l scilicet ipse p excedit eum, qui ex f in l, in ipso numero l quandoquidem fg differunt unitate. Ergo, qui fit ex g in l scilicet p excedit ipsum n qui ex f in h, in triplo ipsius l. Eodemque processu ostendam, quod excessus n quo superat ipsum m triplus erit ipsius h quodque excessus m super k triplus erit ipsius f quodque excessus ipsius k super c triplus erit ipsius c. Nam c quia ternarius, triplus tandem per se constat esse ad a unitatem. Et perinde ipse p qui constat ex aggregatione dictorum quatuor excessum et ex c triplus erit [A:60v] ad aggregatum ex ipsis lhfca. Et similiter procedemus in quotcumque propositis numeris eodem processu dispositis. Quod erat demonstrandum.
|
|
15a
211 Rursus, aliterque demonstrare quod cubus sive quadrata columna cum quadrato et triangulo collateralibus coniuncta triplum efficit suae quadratae pyramidis.
212
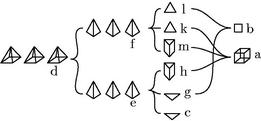
Esto cubus a, quadratus eius b et ![]() lus c, quadrata pyramis d.
lus c, quadrata pyramis d.
213
Dico quod cumulus ex abc factus est triplus ad ipsum d. Quod sic patet. Pyramis d constat ex sua pyramide ![]() la collaterali quae sit e et ex pyramide
la collaterali quae sit e et ex pyramide ![]() la immediate praecedenti quae sit f ut constitit. Itaque triplum ipsius d aequale erit aggregato ex triplo ipsius e triploque ipsius f. Sit g
la immediate praecedenti quae sit f ut constitit. Itaque triplum ipsius d aequale erit aggregato ex triplo ipsius e triploque ipsius f. Sit g ![]() lus ipsi c
lus ipsi c ![]() lo aequalis: et h columna
lo aequalis: et h columna ![]() la100 eidem collateralis: itemque sint
la100 eidem collateralis: itemque sint ![]()
![]() li proxime inferiores et invicem aequales, ipsi kl, et eorum columnis collateralis, proxime scilicet inferior pyramide h et collateralis pyramidi
li proxime inferiores et invicem aequales, ipsi kl, et eorum columnis collateralis, proxime scilicet inferior pyramide h et collateralis pyramidi ![]() lae f. Eritque per praecedentem, columna
lae f. Eritque per praecedentem, columna ![]() la h cum duobus suis triangulis cg simul aequalis triplo pyramidis
la h cum duobus suis triangulis cg simul aequalis triplo pyramidis ![]() lae e. Nec non [A:61r] columna
lae e. Nec non [A:61r] columna ![]() la m pariter cum duobus suis triangulis kl similiter triplo suae pyramidis
la m pariter cum duobus suis triangulis kl similiter triplo suae pyramidis ![]() lae f aequalis: verum ut in primordiis arithmeticae patuit, cubus a aequalis est aggregato columnarum hm et trianguli k. Quadratus autem b ex composito triangulorum gl conflatur. Igitur si pro columnarum hm et triangulorum gkl aggregato sumatur cubus a cum
lae f aequalis: verum ut in primordiis arithmeticae patuit, cubus a aequalis est aggregato columnarum hm et trianguli k. Quadratus autem b ex composito triangulorum gl conflatur. Igitur si pro columnarum hm et triangulorum gkl aggregato sumatur cubus a cum ![]() to b iam erit aggregatum ex cubo a quadratoque b trianguloque101 c aequale aggregato columnarum102 hm ac triangulorum cgkl. Sed huiusmodi aggregatum columnarum hm et triangulorum cgkl aequale fuit aggregato ex triplo pyramidis e triploque pyramidis f et103 perinde aequale triplo quadratae pyramidis d. Ergo et triplum quadratae pyramidis d aequale erit cumulo, qui ex cubo a quadrato b trianguloque c constabat. Sicut erat demonstrandum.
to b iam erit aggregatum ex cubo a quadratoque b trianguloque101 c aequale aggregato columnarum102 hm ac triangulorum cgkl. Sed huiusmodi aggregatum columnarum hm et triangulorum cgkl aequale fuit aggregato ex triplo pyramidis e triploque pyramidis f et103 perinde aequale triplo quadratae pyramidis d. Ergo et triplum quadratae pyramidis d aequale erit cumulo, qui ex cubo a quadrato b trianguloque c constabat. Sicut erat demonstrandum.
214 Ecce multo brevius ac facilius in praesenti propositione ostensum est id, quod in prima propositione fuerat ex traditione Archimedis demonstratum. Rursum igitur ex hac possunt demonstrari 2a et 3a propositiones, quae per primam demonstratae sunt: et sequentes 4a et 5a ex his postea demonstrate. Item et 7a quae per 2am. Quam ob rem 8a 9a 10a 11a 12a 13a 14a et praesens 15a essent in principio ponendae. Quoniam concatenatae sunt in ordine de [A:61v] monstrandi. Sic in hoc et in aliis duobus arithmeticae nostrae libellis, quos antea scripseramus, supplevimus ea, quae Boetius et Iordanus circa formas numerarias omiserant.
215 Catanae 6 novembris 1553.