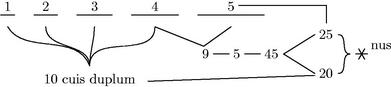
220 Et quod in prima tabella de hexagonis primi ordinis promiseramus sic demonstrabimus. Hoc est ex ductu radicum in impares fieri collaterales hexagonos primi ordinis. Nam, cum, ut ex constitutione ipsius hexagoni constat, hexagonus fiat ex collaterali duploque praecedentis ^li: cumque ex proposita radice in¹⁰⁵ aggregatum sui cum radice immediate praecedenti, hoc est, in imparem collateralem, fiat aggregatum ex ^to propositae radicis et ex duplo cumuli praecedentium omnium radicum, hoc est ex duplo praecedentis ^li per regulam progressionis: iam ex tali ductu fiet ipse hexagonus. Sicut proponitur demonstrandum.