[S:149]

PROPOSITIO XXI.

Centrum gravitatis sectionis conicae, quae vocatur parabola, propinquius est vertici, quam centrum gravitatis figurae perspecte inscriptae in sectione.

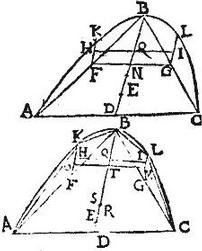
Esto parabole ABC, cuius basis AC diameter BD, in qua super eandem basim, circaque eandem diametrum triangulum describatur ABC, sitque sectionis centrum Q trianguli ABC centrum E, in diametro enim est utrumque, per 19. huius, et per demonstrata in praecedenti libro. Dico itaque quod Q propinquius est vertici, quam E: nam sectis per medium rectis AB, BC in punctis F, G. Ductisque diametris FK, GL; erunt per 19. huius, centra portionum AKB, BLC in diametris KF, LG. Sint talia centra puncta H, I, et coniuncta HI secet ipsam diametrum BD in puncto Q; et coniuncta FG secet eandem in puncto N, eruntque HQ QI aequales. Et quoniam AKB, BLC, portiones aequales, et spatia HQ QI aequalia: idcirco per 16. primi, aequalium momentorum, Q punctum erit commune centrum ipsarum portionum AKB, BLC. Cum autem E sit centrum trianguli ABC erit per 24. praecedentis libri, DE pars tertia ipsius BD, cuius dimidium est DN; itaque Q punctum propinquius vertici, quam E punctum; et ideo cum portionum AKB, BLC tanquam unius partis centrum sit Q: trianguli autem ABC tanquam alterius partis centrum sit E, iam per 6. primi aequalium momentorum, centrum totius, hoc est ipsius sectionis ABC centrum erit in linea EQ coniungente centra partium, et perinde propinquius erit vertici quam E centrum trianguli ABC: quod erat demonstrandum. Rursum inscribatur in eadem sectione ABC perspecte pentagonum AKBLC; rursum dico quod et pentagoni AKBLC centrum propinquius est vertici, quam centrum trianguli ABC remotius vero a vertice, quam centrum sectionis ABC. Hoc modo, cum centra portionum AKB, BLC sint puncta H, I, iam ut dudum ostensum est, centra triangulorum AKB, BLC erunt inferiora ipsis H, I, punctis; sint O, M puncta; et coniuncta OM secet BD apud T, eritque per 16. primi, dictam T centrum commune triangulorum AKB, BLC, tanquam unius partis: sed centrum trianguli ABC tanquam alterius partis est E; igitur totius compositi, figurae scilicet rectilineae AKBLC centrum est in linea ET, sit in puncto R, eritque per 27. primi, aequalium momentorum sicut TR ad RE, sic triangulum ABC ad triangula AKB, BLC. Item portionum AKB, BLC tanquam unius partis commune centrum fuit Q; trianguli ABC tanquam alterius partis centrum E: igitur totius compositi, sectionis scilicet ABC totalis centrum in linea EQ. Sit in puncto S; eritque per 27. praedictam, QS ad SE, sicut triangulum ABC ad portiones AKB, BLC: sed maiorem habet rationem triangulum ABC ad triangula AKB, BLC, quam ipsum idem triangulum ABC ad portiones AKB, BLC: ergo maior est ratio TR ad RE, quam QS ad SE; et coniunctim maior est ratio TE ad ER, quam QE ad ES; et a [S:150] fortiori, maior est ratio TE ad ER, quam TE ad ES. Igitur maior ES quam ER: et propterea S centrum sectionis ABC propinquius est vertici, quam R centrum pentagoni perspecte inscripti in sectione; estque centrum pentagoni inter E centrum trianguli ABC, et S centrum sectionis; sicut erat demonstrandum. Idipsum de omni rectilineo intra parabolam perspecte inscripto demonstrabimus. Unde si novem laterum rectilineum in parabola ABC perspecte inscribatur, per eadem ostendemus talis rectilinei centrum interiacere punctis R, S; et similiter deinceps in reliquis.

SCHOLIUM.

Notandum, quod in libro Archimedis de quadratura parabolae ostensum est, quod omnis portio sub peripheria parabolae, et recta linea comprehensa est sesquitertia ad triangulum super eandem basim, et sub eodem vertice constitutum; hoc est, quod sectio AKBLC sesquitertia est ad triangulum ABC. Itemque sectio AKB sesquitertia est ad triangulum AKB: et similiter sectio BLC sesquitertia ad triangulum BLC. Et quoniam triangula AKB, BLC sunt invicem aequalia, quando eorum utrumlibet est trianguli ABC pars octava, sicut in dicto libro ostenditur. Ideo, et portiones ipsae AKB, BLC sunt aequales, et utralibet earum totius sectionis AKBLC pars octava.

Unde ambo triangula AKB, BLC sunt quarta pars trianguli ABC. Et similiter quatuor triangula in relictis portionibus perspecte inscripta sunt quarta pars triangulorum AKB, BLC: et octo triangula in relictis facta, sunt quarta pars quatuor triangulorum praecedentium, et sic in infinitum. Relictae autem ultimo portiones semper sunt pars tertia triangulorum postremo inscriptorum: et sic fit ut tota sectio sit iam sesquitertia trianguli primi: nam si fuerint quotlibet magnitudines in proportione continua quadrupla, congeries earum, cum tertia parte minime semper est sesquitertia ad maximam: quae cum singula in libello superius memorato sint demonstrata; inde sumenda sunt: sicut et ex conicis elementis quidquid oportunum est, hic adductum citatur.