4^a

16 Circulus aequalis est trigono²⁶ rectangulo cuius, quae quidem ex centro aequalis est uni earum, quae circum rectum angulum, perimeter autem basi.

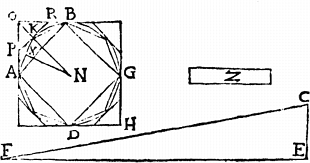
Sit circulus abgd et²⁷ trigonum rectangulum e²⁸ sitque semidiameter circuli abg aequalis uni laterum trianguli e²⁹ quae circum rectum angulum³⁰, perimeter autem abg aequalis reliquo lateri trianguli e³¹ quod circum rectum angulum.

Aio quod aequalis est circulus abg triangulo e³².

Sit enim, si possibile est, maior circulus trigono in³³ spacio quopiam utpote z et inscribatur circulo per 6^am 4ⁱ quadratum abg sectisque periferiis bifariam inscribatur octogonum akb eritque, per primam huius, triangulum akb maius quam 1/2³⁴ portionis circularis akb et similiter reliqua triangula reliquis portionibus, hoc autem toties faciam, donec per primam 10ⁱ relictae portiones sint minus quam spatium z, itaque inscriptum polygonium akb maius erit trigono e³⁵.

17 Capiatur una perpendicularium a centro circuli n ad latera polygonii akb³⁶ utpote nx perpendicularis ad latus ak eritque, per praecedentem, polygo[A:23v]nium akb aequale [S:29] trigono rectangulo, cuius laterum, quae circa rectum, alterum ipsi nx reliquum perimetro polygonii akb est aequale, sed tale trigonum minus³⁷ trigono e³⁸, quandoquidem trigoni e³⁹ latera, quae circa rectum, maiora sunt utpote quorum alterum semidiametro⁴⁰ circuli abg, quae maior est perpendiculari nx reliquum perimetro circuli, qui maior perimetro polygonii, aequale est. 18 Ergo polygonium akb minus erit trigono e⁴¹, fuit autem maius, quod est impossibile.

Non est ergo circulus abg maior trigono e⁴².

Sit nunc, si possibile est, minor circulus abg trigono e⁴³ in spatio quovis utputa z et circumscribatur circulo, per 7^am 4ⁱ, quadratum oh cuius latera contingant circulum apud puncta a, b, g, d⁴⁴ sectaque periferia akb⁴⁵ bifariam in signo k similiter et reliquis⁴⁶, agatur per k circulum contingens pkr lateribus quadrati circumscripti occurrens apud p, r⁴⁷ et similiter in reliquis tribus⁴⁸ periferiis bg, gd, da; 19 eritque, per 2^am huius, triangulum por maius quam 1/2⁴⁹ figurae aobk quae videlicet sub rectis ao, ob et arcu akb comprehenditur, et similiter reliqua triangula apud angulos quadrati oh maiora quam dimidia reliquarum figurarum, non ergo cessabo ab huiusmodi periferiarum bifaria sectione, donec per primam 10ⁱ figurae⁵⁰ quae a circuli periferiis et lateribus circumscripti polygonii comprehenduntur redigantur ad minus spacium spacio z. 20 Itaque circumscriptum polygonium apkr⁵¹ erit minus trigono e⁵².

Connectatur ergo centrum n cum uno⁵³ [A:24r] punctorum, in quibus latera polygonii apk contingunt circulum, utpote cum puncto k, eritque, per praecedentem, polygonium apk aequum trigono rectangulo, cuius laterum, quae circa rectum, alterum ipsi nk, reliquum perimetro polygonii apk est aequale; huiusmodi ergo trigonum maius est trigono e⁵⁴, quandoquidem trigoni e⁵⁵ laterum quae circum rectum, unum ipsi nk est aequale, reliquum vero perimetro circuli, qui minor est perimetro polygonii apk. 21 Quare polygonium apk maius est trigono e⁵⁶, fuit autem minus, quod est absurdum.

Non est igitur circulus abg minor trigono e⁵⁷, fuitque⁵⁸ ostensum quod nec maior; aequalis ergo erit circulus abg trigono E⁵⁹ quod est propositum.

22 Hinc⁶⁰ manifestum est quod circulus aequalis est rectangulo quod sub semidiametro circuli et linea aequali⁶¹ dimidio periferiae comprehenditur.

Corollarium⁶²

Manifestum est ergo quod ex ductu semidiametri in dimidium periferiae producitur area circuli.