5^a

23 Circulorum diametri sunt periferiis proportionales.

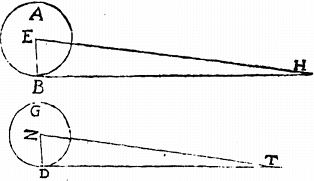
Sunto duo circuli ab, gd, quorum centra ez et semidiametri eb, zd.

Aio quod sicut semidiameter eb ad semidiametrum zd sic periferia ab ad peri[S:30]feriam gd.

Sint enim ipsis eb, zd ad rectos angulos ipsae bh, dt, quarum bh periferiae ab, et dt periferiae gd ponantur aequales, et connectantur eh, zt eritque per praemissam circulus ab trigono ebh et circulus gd trigono zdt aequalis. Sed per 2^am 12ⁱ circulus ab ad circulum gd sicut⁶³ quadratum eb ad quadratum zd. 24 Ergo trigonum ebh ad trigonum zdt sicut⁶⁴ quadratum eb ad quadratum zd. Verum⁶⁵ ratio quadrati eb ad quadratum zd dupla est eius, quae eb⁶⁶ ad zd per 17^am 6ⁱ; igitur ratio trigoni ebh ad trigonum ztd componitur ex duabus rationibus, quarum quaelibet [A:25r] est sicut eb ad zd. 25 Sed eiusdem trigoni ebh ad idem trigonum zdt ratio per 24^am 6ⁱ componitur ex ratione eb ad zd et ex ratione bh ad dt propter angulos b, d⁶⁷ aequales. Necesse est ergo ut ratio eb ad zd sit⁶⁸ sicut bh ad td⁶⁹ et ideo sicut periferia ab ad periferia gd, quod est propositum.