[A:22v]

3^a

10 Polygonium rectilineum, in quo a quopiam interiori puncto ad latera singula perpendiculares sunt invicem aequales (quale est circulo circumscriptum vel aequilaterum circulo inscriptum) aequale est triangulo rectangulo, cuius unum laterum, quae circum²⁰ rectum angulum, aequale est uni perpendicularium praedictarum, reliquum²¹ vero aequale perimetro rectilinei.

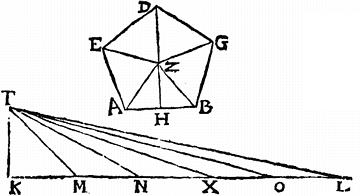
11 Esto rectilinea figura abgde in qua a quodam interno puncto ut pote z ad latera singula perpendiculares sint aequales ducatur autem ad unum laterum ut pote ab perpendi[S:28]cularis zh, sitque triangulum tkl rectum qui apud k angulum habens, cuius latus tk aequum sit perpendiculari zh, latus vero kl aequum sit perimetro figurae abg.

12 Aio quod aequale est polygonium abg triangulo tkl.

Connectantur enim anguli figurae abg²² cum puncto z et dividatur kl in portiones tot, quot sunt latera figurae abg singulas singulis lateribus aequales, quando tota kl universis simul lateribus est aequalis; sitque ipsi ab ipsa km, ipsi bg ipsa mn, ipsi gd ipsa nx, ipsi de ipsa xo, ipsique ea ipsa ol aequalis: et connectantur puncta m, n, x, o²³ cum puncto t.

13 Itaque quoniam triangulorum azb, ktm bases sunt aequales et celsitudines aequales, ideo per primam 6ⁱ aequalia sunt invicem triangula azb, tkm. Similiter et ipsa triangula bzg, mtn invicem, et ipsa gzd, ntx invicem, et ipsa dze, xto invicem, et ipsa eza, otl invicem aequalia erunt. Quare totum rectilineum abg toti triangulo ktl aequum est, quod est propositum. [A:23r]

14 Et attendendum quod in figura circulo circumscripta perpendiculares a centro circuli ad latera figurae sunt aequales, namque rectae a centro ad puncta contactuum²⁴ egredientes sunt per 17^am 3ⁱⁱ ipsis lateribus perpendiculares, quae per diff. circuli, sunt aequales.

15 Item in figura aequilatera circulo inscripta perpendiculares a centro ad latera sunt aequales, quod patet per 13^am 3ⁱⁱ bene²⁵ ergo huiusmodi figuras in exemplum citat propositio.