2^a

5 Si a puncto extra circulum duae linae ducantur circulum contingentes, de figura sub contingentibus et assumpto arcu comprehensa plus quam dimidium abscindet recta, quae circulum contingit apud punctum medium arcus assumpti.

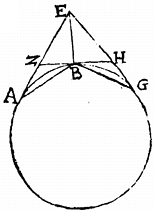
A puncto e extra circulum abg ducantur duae rectae ea, eg contingentes circulum [A:22r] in punctis a, g⁶ et secta bifariam periferia abg in puncto b, agatur per signum b recta zbh circulum contingens et apud zh occurrens ipsis ae, eg.

Aio quod triangulum zeh maius est quam dimidium figurae eabg contentae scilicet sub lineis ae⁷, eg et periferia abg.

6 Connectantur enim rectae ab, be, bg⁸ [S:27] et quoniam ex penultima 3ⁱⁱ ae, eg⁹ sunt aequales, et per 27^am eiusdem, rectae ab, bg, aequales, ideo per 8^am primi triangula aeb, beg sunt invicem aequiangula; igitur anguli zab, hgb aequales. 7 Sed angulus zba aequalis angulo zab et angulus hbg¹⁰ aequalis angulo hgb, quoniam utrumque triangulorum azb, bhg isosceles ex pen. 3ⁱⁱ. Igitur triangula azb, bhg sunt invicem aequilatera per 26^am primi, quare rectae az, gh aequales, et¹¹ ipsae zb, bh aequales. 8 Itemque supersunt ze, eh aequales, unde¹² triangula¹³ bez, beh¹⁴ invicem¹⁵ aequilatera¹⁶ erunt per 8^am primi et aequiangula; et ideo angulus zbe aequalis angulo ebh¹⁷ recti sunt ergo anguli zbe, ebh¹⁸. Itaque per 19^am primi, ez maior quam zb et ideo maior quam az, quare per primam 6ⁱ maius triangulum ebz triangulo zba. 9 Similiter ostendam quod triangulum ebh maius triangulo hbg, igitur totum triangulum zeh maius quam duo triangula zba, hbg simul. Quare triangulum zeh maius quam dimidium triangulorum eba, ebg sed¹⁹ figura eabg minor quam duo triangula eba, ebg. Ergo, a fortiori, triangulum zeh maius quam dimidium figurae eabg comprehensae videlicet sub lineis ae, eg et arcu abg, quod est propositum.

Corollarium

Manifestum est ergo quod quatuor linae az, zb, bh, hg sunt invicem aequales.