47

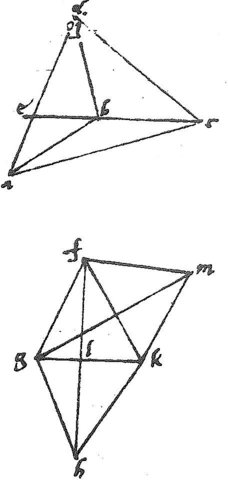
140 Cubus, dodecahedrum, icosahedrum angulariter annexi non totum adhuc undique locum replent. Ut commodius breviusque propositum ostendamus, sicut in 45^o cap. cubi et octahedri coniunximus angulos, ita in praesenti icosahedri simul et dodecahedri angulos ad unam rectam coaptabimus, ut appareat angulum ad loci completionem relictum non posse ab angulo cubi totum impleri. 141 Sit itaque icosahedri quidem angulus abc dodecahedri vero cbd exeuntibus brachiis ab, bc, bd invicem aequalibus: unde producta cb ad e per 5^am et 32^am primi Elementorum, est angulus abd duplus ad angulum acd; duplicabo igitur angulum acd sicut in 45^o cap. feci. Ipsi itaque triangulo abc ipsum fgh atque ipsi triangulo cbd ipsum hkf simile et aequum facio, ita ut ipsi abc angulo ipse fgh angulus et ipsi hkf angulo ipse cbd angulus aequalis sit. 142 Et connexis fh, gk se in signo l secantibus, ipsi kfg triangulo ipsum kfm triangulum simile et aequum statuo, ita ut fg, fm latera sint invicem aequalia, et gk, km aequalia, [A:14r]

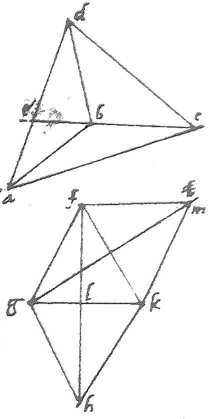
et iis oppositi anguli aequales. Et connexa gm erunt tres anguli ad signum k coëuntes¹²² invicem aequales. Quare anguli hkf et gkm invicem aequales, et triangula hkf, gkm simila. Sed, per 25^um cap. posito quadrato fh 10000 fiet quadratum fg partium 2864 et minus quam 2865. 143 Sed quadratum fl 2500 quoniam scilicet quarta pars quadratum fh: ergo per penultimam primi Elementorum, dempto quadrato fl a quadrato fg, supererit quadratum gl, maius quidem, quam 364, minus quam 365. Item, quoniam positum est quadratum fh partium 10000, fiet per 24^um cap. quadratum ipsius fk maius quam 3454, minus quam 3455. Unde¹²³ dempto quadrato fl, relinquetur quadratum lk, maius quam 954, minus quam 955. Quare linea¹²⁴ gl maior erit quam partes 19, minor quam 191/5: linea vero lk maior quam partes 304/5, minor quam 31. 144 Unde tota gk fiet maior¹²⁵ quam partes 494/5, minor quam 501/5. Inde quadratum ipsius gk, si recte numeres, maius erit, quam partes 2479, minus quam 2510. Sed propter triangulorum kfh, kgm similitudinem, est sicut quadratum kf ad quadratum fh, sic quadratum kg ad quadratum gm, fuitque quadratum fh 10000, quadratum kf maius quam 3454, minus quam 3455. Maior ergo est ratio quadrati¹²⁶ kg ad quadratum gm quam 3454 ad 10000, minor vero quam 3455 ad 10000. Sed sicut 3454 ad 10000, sic 2510 ad 72661618/1727, et sicut 3455 ad 10000, sic 2479 ad 717575/691. 145 Ergo, per 12^am quinti, maior est ratio quadrati kg ad quadratum gm quam 2510 ad¹²⁷ 72661618/1727, minor vero quam 2479 ad 717575/691. Et a fortiori, abiectis fractionibus, maior est ratio quadrati kg ad quadratum gm quam 2510 ad 7267, minor vero quam 2479 ad 7175¹²⁸. Sed 2510 maius est quam quadratum kg et 2479 minus eodem quadrato. Igitur, per 8^am quinti, maior erit ratio 2510 ad quadratum gm quam ratio 2510 ad 7267, quare, per 10^am 5ⁱ, quadratum gm minus est, quam 7267. Et per 8^am 5ⁱ, minor erit ratio 2479 ad quadratum gm quam ratio 2479 ad 7175. 146 Ergo, per¹²⁹ 10^am 5ⁱ, quadratum gm maius est, quam 7175. Cum itaque gm ad fg potentialiter sit maior quam 7175 ad 2865, minor vero quam 7267 ad 2864 et 7175 ad 2865 maiorem habeat rationem, quam duplam: latus autem angulum cubi subtendens ad alterum brachiorum duplam¹³⁰ habeat potentialiter rationem: a fortiori gm ad fg potentialiter maiorem habebit rationem quam latus angulum cubi subtendens ad alterum brachiorum. 147 Sed propter triangulorum similitudinem, sicut gm ad fg [A:14v]ad ad ab (sunt enim triangula gfm abd similia, cum angulus gfm duplus sit ipsius gfk et ideo duplus ipsius acd et ideo aequalis ipsi abd) ergo ad ad ab potentialiter maiorem habebit rationem, quam latus angulum cubi subtendens ad alterum brachiorum. Quare, per 26^um cap. angulus abd maior angulo cubi: angulus ergo cubi non implet angulum abd qui superest post dodecahedri cum icosahedro connexionem. Cubus igitur, dodecahedrum, icosahedrum angulariter compositi non sufficiunt ad locum totum consummandum.