45

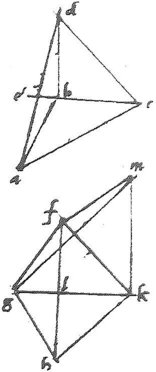
133 Cubus, octahedrum ac dodecahedrum angulariter coniuncti non satis sunt ad locum implendum. Connectemus *** octahedri ac cubi angulos ut pateat relictum spatium maius esse, quam ut a dodecahedri angulo impleatur. Sit itaque octahedri angulus abc cubi autem cbd qui quoniam superant duos rectos, connexa da et angulus abd relictum spatium: et quoniam, sicut in 42^o cap fecimus, ab, bc, bd brachia sunt invicem aequalia, perducta¹¹⁴ cb ad e per 5^am et 32^am primi, angulus abd duplus erit ad angulum acd. 134 Duplicabo igitur angulum acd sicut in 42^o cap. factum est. Nam ipsi triangulo abc ipsum fgh et ipsi triangulo cbd ipsum hkf et aequum¹¹⁵ statuo, ductis fh et kg se invicem in signo l secantibus: ita ut ipsi abc angulo ipse fgh angulus ipsi autem cbd angulo ipse hkf angulus aequalis sit. Mox ipsi kfg triangulo simile et aequum triangulum facio kfm ita ut anguli kfg et kfm sint invicem aequales, et anguli fkg, fkm inter se aequales, et reliquus reliquo et latera lateribus et connexa gm erunt tres anguli ad signum k coëuntes, invicem aequales: quare anguli hkf et gkm invicem aequales: et triangula hkf, gkm similia. 135 Sed, per 23^um cap., posito quadrato fh¹¹⁶ partium 8 fiet quadratum fg¹¹⁷ partium 3 et per 22^um cap. quadratum fk 4: unde quadratum fl 2, quadratum gl unitas. quadratum lk 2: unumquodque enim trium triangulorum hkf, flk, klh est orthogonium habens duo latera rectum comprehendentia invicem aequalia. Erit itaque linea¹¹⁸ gk radix quadrata binarii et unitas: quod quidem binomium in se ductum gignit 3 cum radice octonarii. Quadratum ergo gk erit 3 cum r. 8 quod duplatum facit 6 cum r. 32 et tantum est quadratum gm quoniam angulus gkm rectus, et latera gk, km invicem aequalia. 136 Sed angulus gfm duplus ad angulum gfk et ideo duplus ad angulum acd et ideo aequalis angulo abd. Quare posito quadrato ad 6¹¹⁹ cum r. 32, quantum est quadratum gm tunc erit quadratum ab 3, quantum fuit quadratum fg scilicet radix quadrata 32 est maior quam 56/10, minor vero quam 57/10; quadratum igitur ad quadratum ab maiorem rationem habebit quam 116/10 ad 3, minorem vero quam 117/10 ad 3. 137 Sed maior est ratio 116/10 ad 3 quam 100 ad 34 et 100 ad 34 maior est ratio, per 24^um cap., quam lateris subtendentis angulum dodecahedri ad suum brachium potentialiter: ergo a fortiori da ad ab maiorem habebit rationem potentialiter quam latus subtendens angulum [A:13v]dodecahedri ad brachium suum. Quare per 26^um cap. angulus abd maior est angulo dodecahedri. Sed angulus abd est id, quod superest, spatium post cubi cum octahedro connexionem: igitur cubus, octahedrum et dodecahedrum angulariter coniuncti non totum undique spatium complent.