38

113 Duae pyramides, cum duobus dodecahedris excedunt iustum loci complementum. Connectemus duorum docadedrorum angulos ut videamus an relicto spatio congruant duarum pyramidum anguli ita ut locum impleant.

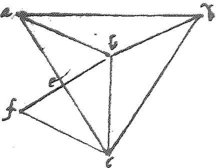
Sint igitur duorum dodecahedrorum anguli abc cbd lineam bc commune ha[A:11r]bentes. Connectatur ab et secta bifariam ac in puncto e ducatur be et extendatur ad f ita ut ipsi be aequalis sit ef et connexa fc fiet ipsi cbe aequale ac simile triangulum cfe⁸⁵ unde bcf angulus ipsi acd angulo aequalis est: atque ideo bcf triangulum ipsi acd triangulo simile fiet. 114 Ex calculo quidem 25^o cap.⁸⁶ patet, quod posito quadrato ac partium 10000, quadratum bc maius erit quam 3454, minus vero quam 3455 quadratum; autem ec est partium 2500, quoniam scilicet quarta pars quadrati ac, unde, per penultimam primi, subtracto quadrato ec de quadrato bc, supererit quadratum eb maius quidem quam 954, minus vero quam 955. Quod si quadrupletur fiet quadratum bf maius quidem quam 3816, minus vero quam 3820. 115 Nunc breviabo numeros, ne praeter necessarium laboremus. Sic posito quadrato ac partium 100 fiet bc maius quam 34 minus vero quam 35 et bf maius quam 38, minus quam 39, de quadrato intellige. Set propter triangulorum similitudinem, sicut quadratum bc ad quadratum bf, sic quadratum ac ad quadratum ad: ergo ratio quadrati ac ad quadratum ad ad maior quidem erit quam 34 ad 39, minor vero, quam 35 ad 38 estque quadratum ac 100. Ex quibus rationibus comperitur quadratum ad maius quidem quam 1084/7, minus vero quam 11412/17, fuitque ab quadratum maius 34 et 35 minus. 116 Ratio ergo quadrati ad ad quadratum ab minor est quam 115 ad 34 et haec rursum minor, quam 32 ad 9, quare multo magis ratio quadrati ad ad quadratum ab, minor est quam 32 ad 9. Sed ratio 32 ad 9 est quadratum ad in figuratione praemissi cap. ad quadratum ab et angulus abd in eadem figuratione componitur ex angulis duarum pyramidum ergo per 26^um cap. angulus compositus ex duobus angulis pyramidis, maior est angulo abd praecedentis figurationis: sed idem abd angulus est, qui superest a coniunctione duorum dodecahedrorum⁸⁷, ergo duae pyramides cum duobus dodecahedris excedunt iustum loci complemento.