37
109 Duae pyramides cum duobus octahedris praecise locum implent. Quamvis hoc per 15um satis pateat, ostendetur et hic aliter, ut omnis coniunctionum varietas hic percurratur, et nullus adversariis calumniandi locus relinquatur. [A:10v]Coniungemus itaque duos pyramidis angulos, et deinde totidem angulos octahedri, ut ex triangulorum similitudine pateat geminum pyramidis angulum id totum praecise implere, quod gemina octahedra medium relinquunt.
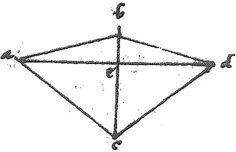
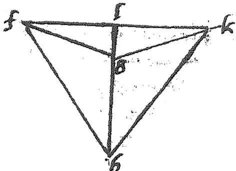
110 Sint ergo anguli duo duarum pyramidum abc, cbd et connectatur ad quae secet ipsam bc in puncto e cum itaque, per 21um cap. ac per potentiam sesquitertia sit ad ab vel ad bc. ideo, si sit quadratum ac *** partium 12, fiet ab vel bc partium 9; dempto igitur *** quadrato ab de quadratis bc, ac, hoc est de 21 supererunt 12, cuius dimidium scilicet 6 erit, per 13am 2i Elementorum, id quod fit ex bc in ce. Secentur ergo 6 in bc, hoc est in 3, et provenient 2, quanta est ce quadratum. Ergo ipsius ce 4, quo dempto de quadrato cd, hoc est de 12, supersunt 8 quadratum, scilicet ed vel ae: totius itaque ad quadrati fiet 32. 111 Sed quadratum ab fuit 9: habemus itaque colligantiam anguli abd ex duobus angulis pyramidis compositi. Nunc sint duorum octahedrorum anguli fgh, hgk et connexa fk producatur hg usque ad l. Cum itaque, per 23um cap. fh sit ad fg potentialiter, sicut 8 ad 3. Ideo posito quadrato fh partium 24, fiet fg vel gh partium 9; demptis igitur quadratis fg, gh, hoc82 est 18 de quadrato fh, scilicet 24 supererunt 6. Cuius dimidium scilicet 3 erit, per 12am 2i Elementorum, id quod fit ex hg in gl. 112 Secentur ergo 3 in gh, hoc est in 3, et prosiliet unitas, quanta est gl; quadratum ergo gl unitas qua dempta de quadrato fg supersunt 8 quadrata scilicet fl vel lk: totius itaque fk quadratum fiet 3283, unde patet triangulum fgk simile esse triangulo abd. Congruet itaque triangulum abd triangulo fgk. Sic84 angulus abc constat ex angulis duarum pyramidum: angulus autem fgk est complementum duorum angulorum octahedri ad quatuor rectos. Sequitur ergo, ut duae pyramides cum duobus octahedris totum praecise locum impleant.