39

117 Una pyramis cum tribus dodecahedris, vel cum tribus icosahedris praeiustum loci complementi. Vestigabo primum quid tres dodecahedri anguli spatii occupent, ut pateat relictum vacuum non esse satis pyramidis angulo capiendo. Id autem hoc ingenio scrutabimur.

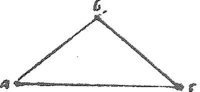
Capio angulum pentagoni aequilateri et aequianguli abc duobus aequis brachii, ab, bc contentum, cui subtendo [A:11v]latus ac quo posito partium 1000000 seco hunc numerum secundum per mediam extremamque rationem, per 11^am 2ⁱ, eritque maius segmentum maius quidem quam 618033 minus vero quam 618034 unde quadratum ac erit 1000000000000: quadratum vero ab maius quidem quam 381964789089, minus vero quam 381966025156.

118 Sed quid opus est toto atomis, cum multo minores numeri possint id praestare, quod volumus. Iam posito quadrato ac partium 100, fiet quadratum ab, maius quidem 38, minus vero 39 cuius quidem calculi causam bene videt, qui 11^am 13ⁱ Elementorum optime cognovit. Angulus itaque b pentagoni aequilateri atque aequianguli valet rectum et quintam recti partem, per 32^am p.ⁱ. 119 Sed in 24^o cap. quadratum kl ad quadratum kd minorem habet⁸⁸ rationem quam 100 ad 34, sed haec maior ratione quadrati ac ad quadratum ab, quippe quae ad summum est sicut 100 ad 38; a fortiori ergo ratio quadrati kl ad quadratum kd maior est quam ratio quadrati ac ad quadratum ab; ergo, per 26^um cap. angulus kdl, qui angulus est dodecahedri⁸⁹, maior est angulo b qui continet rectum et quintam recti. Unde fit ut tres anguli dodecahedri consument plus quam tres rectos et tres quintas recti: relinquitur ergo ad quatuor rectorum complementum minus quam duae quintae unius recti, sed angulus⁹⁰ pyramidis excedit duas quintas recti, ergo⁹¹ pyramis⁹² cum⁹³ duobus dodecahedris excedunt iustum loci complementum. 120 Sed quod pyramidis⁹⁴ angulus excedit duas quintas recti, patet, nam unus huiusmodi angulorum, ut novisti per 27^um cap. superat angulum trianguli aequilateri, qui continet, duas tertias recti. Idem multo magis ostendemus de duobus icosahedris, cum icosahedri angulus angulo dodecahedri sit expansior, sicut patet ex ratione laterum angulos subtententium ad sua brachia.