V. Hyperbole in quolibet cono ab aequidistantibus planis factae, sunt inter se similes.

Sit conus, cuius basis circulus ag; vertex b; et sectus plano per axim ad basim recto faciat triangulum abg; secetur duobus planis parallelis ductis per lineas de, zb ad rectos ipsi ag; et facientibus in cono sectiones zk, dt; quarum axes et, bk, coincidant lateribus conicis apud l, m puncta. Eruntque, per 12. p. conicorum, ipsae sectiones dt, zk hyperbolae.

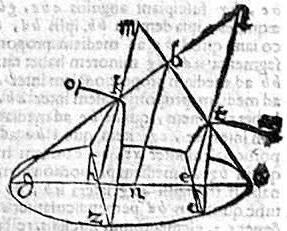
Aio itaque quod similes sunt hyperbolae dt, zk. Ducatur enim ipsis et, hk aequidistans bn. Et sicut est quadratum bn ad rectangulum ang, sic sit tam lt ad tx; quam mk ad ko, proportionales igitur erunt ipsae lt, mk hyperbolarum dt, zk transversae, ipsis tx, ko rectis earumdem diametris. Ergo per 3. huius similes sunt ipsae dt, zk hyperbolae. Quod iam proponitur demonstrandum.

Unde si talium hyperbolarum diametri sint aequales ipsae sectiones inter se similes, et aequales erunt. Aio; idem sequetur quo ad similitudinem si ad easdem partes lineae bn, hoc est super idem coni latus deducantur.