VI. Circulus habens eumdem axim, ac verticem cum hyperbola; diametrumque ipsius rectae aequalem: in solo vertice sectionem tangens, totus intra eam cadit.

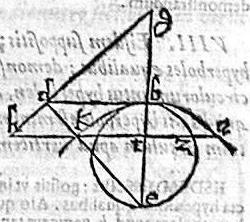
Sit hyperbole ab, cuius transversa bg; rectaque diametros bd, cui aequalis ex axe capiatur be; super qua ut diametro circulus describatur bze. Aio igitur quod circulus bze hyperbolen apud solum b tangit, totusque intra sectionem cadit. Capiatur enim in peripheria circuli quodvis gunctum z, per quod ordinate ducatur azth, coincidens hyperbole quidem apud a; axi apud t, ipsique gd, coniunctae, ac productae apud h punctum; nec non ipsi ed apud k. Et tunc per 12. primi conicorum, at poterit rectangulum bth, ipsa vero xt poterit in circulo rectangulum bte, quod est ipsum rectangulum btk, quod minus est rectangulo bth, quare brevior erit zt, quam at, et perinde punctum z in peripheria circuli existens, cadit intra sectionem. Et similiter omnia puncta peripheriae circuli; atque tota omnino peripheria circuli, excepto b puncto, cadet intra sectionem, et hoc est quod proponebatur demonstrandum.