[S:166] XXIV. Contra, eisdem manentibus: demonstrandum est quod talis hyperbola inter hyperbolas circa eamdem ipsam transversam descriptas, et extrinsecus talem parabolam tangentes, minima est; hoc est minimam rectam diametrum habet.

Hoc est in eadem 21. descriptione: demonstrandum est quod hyperbola ab, inter hyperbolas habentes eam ipsam transversam bg; ac tangentes apud b parabolam bz extrinsecus, minima est; hoc est rectam diametrum minima habet.

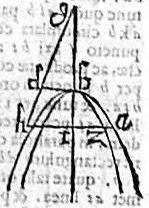
Namque per primam huius, omnis hyperbole habens transversam bg; atque rectam maiorem quam bd. Cadit enim ipsam hyperbolen ab, ipsam tangens; et perinde extra parabolen zb ipsam tangensper 22. autem huius, omnis hyperbole habens rectam minorem ipsa bd, et circa bg transversam posita, secat parabolam bz intra ipsam partim incedens. Igitur inter hyperbolas habentes transversam bg, et extrinsecus tangentes parabolen bz, ipsa hyperbole ab minima est; hoc est minimam rectam, que est bd, habet. Quod fuit demonstrandum.

SCHOLIUM.

Notandum tamen quod sicut omnis hyperbole habens eam ipsam rectam diametrum bd, transversamque breviorem quam bg, cadit per 2. huius, extra hyperbolen ab; et perinde extra parabolen bz, utramque tangens apud b verticem ita omnis hyperbole habent ipsammet rectam bd. Atque transversam longiorem, quam bg, cadit per dictam 2, intra hyperbolen ab, extra vero parabolen bz, 21. huius, unde quamvis inter peripherias hyperboles ab, atque paraboles bz nulla intercidat parabola. Tamen inter easdem infinitae cadere possunt hyperbolae, habentes videlicet rectam bd, transversamque ipsa bg longiorem.