|
1 35a Iisdem existentibus; si a relicto puncto linea quaedam ducatur secans sectionis periferiam apud duo puncta; erit, ut tota ad eam, quae extra recipitur; sic portiones intus receptae hinc inde a periferia ad aequidistantem non tangenti ductam per tactum.
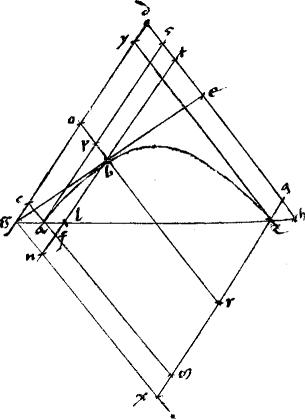 2 Sit hyperbole ab. // Non tangentes gde. // Tangens gbe. // Ipsi dg aequidistans tblfn. // Ipsa autem galzh secet periferiam sectionis apud a z puncta. // Dico iam quod ut est zg
2 Sit hyperbole ab. // Non tangentes gde. // Tangens gbe. // Ipsi dg aequidistans tblfn. // Ipsa autem galzh secet periferiam sectionis apud a z puncta. // Dico iam quod ut est zg  ga sic erit zl ga sic erit zl  la. // Ducantur enim aequidistantes ipsi de non tangenti, lineae gnx cafm opbr zy. // aequidistantes autem ipsi gd alteri non tangentium, [A:85r] lineae aps qzrmx1. 3 // Et quoniam, per 8am secundi Conicorum ag aequalis zh erit propter similitudinem triangulorum ipsa ca aequalis qh. // Sed propter aequidistantiam linearum ds aequalis ca. // Ergo qh aequalis ds. // Et simili ratione gc aequalis dy. // Quare et dc [S:114] aequalis gy. // Ut igitur dc la. // Ducantur enim aequidistantes ipsi de non tangenti, lineae gnx cafm opbr zy. // aequidistantes autem ipsi gd alteri non tangentium, [A:85r] lineae aps qzrmx1. 3 // Et quoniam, per 8am secundi Conicorum ag aequalis zh erit propter similitudinem triangulorum ipsa ca aequalis qh. // Sed propter aequidistantiam linearum ds aequalis ca. // Ergo qh aequalis ds. // Et simili ratione gc aequalis dy. // Quare et dc [S:114] aequalis gy. // Ut igitur dc  cg sic gy cg sic gy  cg. // Et propter similitudinem triangulorum sicut gy cg. // Et propter similitudinem triangulorum sicut gy  cg sic zg cg sic zg  ga et sic mc ga et sic mc  ca. // 4 Per primam autem 6i Euclidis ut mc ca. // 4 Per primam autem 6i Euclidis ut mc  ca sic ca sic  mcd mcd   acd. // Utque dc acd. // Utque dc  cg sic cg sic  dcf dcf   cgn2. // Igitur sicut cgn2. // Igitur sicut  dcf dcf   cgn sic cgn sic  mcd mcd   acd. // Per 12am autem secundi Conicorum, aequale acd. // Per 12am autem secundi Conicorum, aequale  acd ipsi acd ipsi  bod hoc est ipsi bod hoc est ipsi  bng. 5 (Sunt enim bng. 5 (Sunt enim   bod bng aequalia, cum, per 3am secundi Conicorum gb be et ideo, per 2am 6i Euclidis do og sint aequales). Ut ergo bod bng aequalia, cum, per 3am secundi Conicorum gb be et ideo, per 2am 6i Euclidis do og sint aequales). Ut ergo  mcd mcd   bng totum scilicet ad totum, sic iam erit bng totum scilicet ad totum, sic iam erit  dcf dcf   cgn ablatum videlicet ad ablatum. 6 // Quam ob rem, per 19am quinti Euclidis sic etiam erit cgn ablatum videlicet ad ablatum. 6 // Quam ob rem, per 19am quinti Euclidis sic etiam erit  mft mft   bfc relictum ad relictum. // Et quoniam, per 12am 2i Conicorum bfc relictum ad relictum. // Et quoniam, per 12am 2i Conicorum  cds aequale cds aequale  tbo. // Commune auferatur tbo. // Commune auferatur  pod. // Et supererit pod. // Et supererit  cop aequale cop aequale  pst. // Commune apponatur pst. // Commune apponatur  apb. // Fietque apb. // Fietque  cfb aequale cfb aequale  ast. // Igitur sicut ast. // Igitur sicut  mcd mcd   acd sic acd sic  mft mft   ast. 7 // Fuit autem ut ast. 7 // Fuit autem ut  mcd mcd   acd sic mc acd sic mc  ca hoc est zg ca hoc est zg  ga (3 propter similitudinem triangulorum)4. // Atque, per primam sexti Euclidis ut ga (3 propter similitudinem triangulorum)4. // Atque, per primam sexti Euclidis ut  mft mft   ast sic mf ast sic mf  fa hoc est zl fa hoc est zl  la (5 propter similitudinem triangulorum )6. // Ergo iam zl la (5 propter similitudinem triangulorum )6. // Ergo iam zl  la 7 sicut zg la 7 sicut zg  ga. // Quod fuit demonstrandum. ga. // Quod fuit demonstrandum.
|
