|
1 33a Si contrapositas lineae tangentes coincidant: tactusque linea coniungat: perque concursum tangentium ducatur linea penes iungentem tactus: atque per medium punctum iungentis tactus ducatur linea penes unam non tangentium coincidens sectioni et ductae1 per concursum aequidistanti: tunc, quae est inter medium punctum et aequidistantem, per aequalia secatur a periferia sectionis.
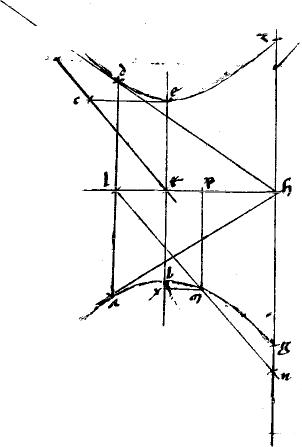 2 Sint contrapositae abg2 dez. // Tangentes ahd. // Centrum t. // Non tangens tc. // Et coniungatur th. // Quae, per 39am secundi Conicorum, producta bifariam secabit ipsam ad ut pote ad l. // Item bte3 zhgn aequidistantes ipsi ad iungenti tactus. // Ipsaque lm aequidistans ipsi tc occurrat sectioni apud m ipsique zhg apud n. // Dico iam quod ln per medium secatur apud m. 3 // Sint enim ec mx aequidistantes ipsi ht secundae diametro et perinde [A:84r] ad ipsam ab4 primam applicatae. // Eritque per 21am primi Conicorum
2 Sint contrapositae abg2 dez. // Tangentes ahd. // Centrum t. // Non tangens tc. // Et coniungatur th. // Quae, per 39am secundi Conicorum, producta bifariam secabit ipsam ad ut pote ad l. // Item bte3 zhgn aequidistantes ipsi ad iungenti tactus. // Ipsaque lm aequidistans ipsi tc occurrat sectioni apud m ipsique zhg apud n. // Dico iam quod ln per medium secatur apud m. 3 // Sint enim ec mx aequidistantes ipsi ht secundae diametro et perinde [A:84r] ad ipsam ab4 primam applicatae. // Eritque per 21am primi Conicorum  te te   ec sicut ec sicut  bxe bxe   xm5. xm5. |
|
|
Et coniunctim sic etiam |
 bxe bxe |
 |
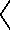 |
 xm xm |
. |
 te te |
 ce ce |
|
|
6. Verum  ce aequale ce aequale  7 htl per 38am primi Conicorum, cum ce sit 1/2 secundae diametri ut in 31am huius. // 4 Ductaque mp penes bt et ad erit xm8 aequalis tp. // Et tx9 aequalis mp. 7 htl per 38am primi Conicorum, cum ce sit 1/2 secundae diametri ut in 31am huius. // 4 Ductaque mp penes bt et ad erit xm8 aequalis tp. // Et tx9 aequalis mp. |
|
// Per 6am autem secundi Euclidis  tx10 hoc est tx10 hoc est  mp aequale est mp aequale est |
11 |
. |
|
|
|
|
// Igitur sicut  te te   ec sic ec sic  tx sive12 mp tx sive12 mp |
|
simul. |
|
|
5 // Propter autem similitudinem ac proportionem triangulorum ut  te te   ec sic ec sic  mp mp   pl. pl. |
|
// Ergo, sicut  mp mp   pl sic pl sic  mp mp |
|
simul. |
|
|
|
|
// Quare, per 9am quinti Euclidis  pl aequale est pl aequale est |
|
simul sumptis. |
|
|
6 // Itaque, adducto lemmate, quod praecessit 31am huius lh per medium secatur apud p. // Sed aequidistat pm ipsi hn. // Igitur per 2am sexti Euclidis et ipsa ln non secus, per aequalia secatur apud m. // Quemadmodum proponitur demonstrandum.
|
