|
[A:68r] 10a Iisdem subiectis, relicta puncta cl sint iam extra incidentias diametrorum: ipsique tangenti bh sint aequidistantes cxi, kl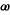 . // Tangenti autem gn aequidistantes lym, kcr. // Diametris aihegy . // Tangenti autem gn aequidistantes lym, kcr. // Diametris aihegy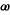 1 et2 dmnezbxr3 existentibus: demonstrandum est, quod quadrilaterum rmlk aequale est quadrilatero ci 1 et2 dmnezbxr3 existentibus: demonstrandum est, quod quadrilaterum rmlk aequale est quadrilatero ci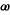 k. k.
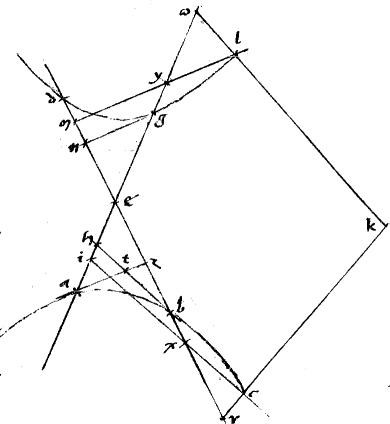 1 Namque, cum bh tangens coincidat diametro aeg ad quam diametrum ordinata est atz tangens apud summitatem a et coincidens ipsi deb per centrum et tactum b ductae. Et a relicto puncto c in sectione agantur ad diametrum aeg duae lineae cxi quidem penes bh tangentem: cr autem penes ordinatam az sive (quod idem est) penes ordinatam a tactu b4. // Propterea iam per 43am primi Conicorum,
1 Namque, cum bh tangens coincidat diametro aeg ad quam diametrum ordinata est atz tangens apud summitatem a et coincidens ipsi deb per centrum et tactum b ductae. Et a relicto puncto c in sectione agantur ad diametrum aeg duae lineae cxi quidem penes bh tangentem: cr autem penes ordinatam az sive (quod idem est) penes ordinatam a tactu b4. // Propterea iam per 43am primi Conicorum,  xei est xei est   lis xrc beh simul sumptis. 2 // Item quoniam in contrapositis, ipsi az sive5 (quod idem est) ipsi a tactu b6 ordinatae, per7 summitatem g alterius sectionis aequidistans ducitur ng coincidens ipsi deb per centrum, [S:91] tactumque b ductae: et a relicto puncto l in sectione aguntur ad diametrum aeg duae lineae l lis xrc beh simul sumptis. 2 // Item quoniam in contrapositis, ipsi az sive5 (quod idem est) ipsi a tactu b6 ordinatae, per7 summitatem g alterius sectionis aequidistans ducitur ng coincidens ipsi deb per centrum, [S:91] tactumque b ductae: et a relicto puncto l in sectione aguntur ad diametrum aeg duae lineae l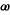 quidem penes bh tangentem. lym vero penes ipsam az sive (quod idem est) penes ordinatam a tactu b8. 3 // Ideo iam, per 44ae primi Conicorum quidem penes bh tangentem. lym vero penes ipsam az sive (quod idem est) penes ordinatam a tactu b8. 3 // Ideo iam, per 44ae primi Conicorum  mye aequale est mye aequale est   y y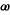 l, eaz pariter acceptis. //Sunt autem, per primam huius, l, eaz pariter acceptis. //Sunt autem, per primam huius,   beh aez aequalia; et ideo, quanto maius est beh aez aequalia; et ideo, quanto maius est  lum xei lum xei  lo xrc tanto maius est lo xrc tanto maius est  lum mye lum mye  lo y lo y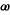 l. //Igitur l. //Igitur   xei y xei y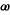 l simul sumpta aequalia sunt ipsis l simul sumpta aequalia sunt ipsis   mye, xrc similiter sumptis. 4 // Commune itaque tam his, quam illis triangulis apponatur sexangulum cxeylk. Fientque, si attendis, duo tetragona invicem aequalia, videlicet mye, xrc similiter sumptis. 4 // Commune itaque tam his, quam illis triangulis apponatur sexangulum cxeylk. Fientque, si attendis, duo tetragona invicem aequalia, videlicet  [[rum]]9 ci [[rum]]9 ci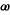 k aequale k aequale  [[ro]]10 rmlk. // Et hoc est, quod demonstrandum proponebatur. [[ro]]10 rmlk. // Et hoc est, quod demonstrandum proponebatur.
|
![]() . // Tangenti autem gn aequidistantes lym, kcr. // Diametris aihegy
. // Tangenti autem gn aequidistantes lym, kcr. // Diametris aihegy![]() 1 et2 dmnezbxr3 existentibus: demonstrandum est, quod quadrilaterum rmlk aequale est quadrilatero ci
1 et2 dmnezbxr3 existentibus: demonstrandum est, quod quadrilaterum rmlk aequale est quadrilatero ci![]() k.
k. 