Quo pacto columnae fiant triplae ad pyramides. Caput 3^um123.

Calagurae¹²⁴.

243 Omnis columna ^la 2ⁱ ordinis cum et cum collateralibus primi ordinis coniuncta triplum facit suae pyramidis.

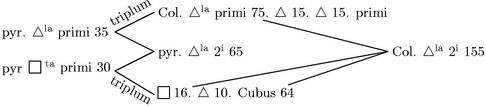
Sumatur columna ^la 155 2ⁱ ordinis cum 25 et ^lo 15 coniuncta: quod facit 195. Aio quod 195 triplum est pyramidis 65. Nam per caput antepraemissum pyramis 65 ^la125 2ⁱ conflatur ex pyramide ^la 35 primi ordinis collaterali et ex pyramide eiusdem ordinis praecedenti 30¹²⁶ . Sed per 14^am praecedentium columna ^la 75 primi cum duplo sui ^li hoc est cum 30, facit triplum pyramidis 35¹²⁷. Et, ut in principio fuit ostensum, cubus 64 cum suo ^to 16 ac ^lo 10 facit etiam triplum pyramidis ^tae praedictae 30.

244 Igitur columna ^la 75 cum duplo ^li 15 cumque cubo 64, ^to 16 atque ^lo 10 totum hoc faciet pyramidis praedictae 65 triplum.

245 Sed per praemissum caput, columna ^la 75 cum cubo 64 et ^to 16 format columnam ^lam propositam 155.

246 Ergo columna ^la proposita 155 cum duplo ^li 15 et ^lo praecedenti 10 faciet¹²⁸ id ipsum triplum. Verum, ut in arithmeticis ostendebatur ^la 10 15 faciunt ^tum 25.

247 Itaque et columna proposita ^la 155 cum collaterali 25 et ^lo collaterali 15 faciet dictum suae pyramidis ^lae 65 triplum, quod est 195. Quod fuit demonstrandum.

248 Igitur columna ^la 155 2ⁱ ordinis cum 15, 15, 10, hoc est cum

249

25 15

conflabat 195, triplum suae pyramidis ^lae 65. Quod est propositum.

250 Omnis columna ^ta 2ⁱ ordinis cum duplo ^ti collateralis in primo ordine coniuncta conflat triplum suae pyramidis.

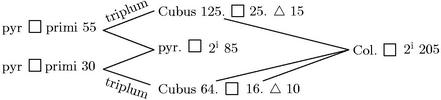
251 Sumatur columna 205 2ⁱ ordinis cum duplo ^ti 25, scilicet 50, faciens iam 255. Aio quod 255 triplus est pyramidis suae ^tae 85. Nam per caput antepraemissum pyramis 85 2ⁱ conflatur ex pyramide 55 primi collaterali et ex pyramide 30 praecedenti in primo ordine. Sed per 15^am praecedentium, cubus 125 cum 25 et 15 facit triplum pyramidis 55 primi. Et ut in principio fuit ostensum: cubus 64 cum 16 et 10 facit adhuc triplum pyramidis praedictae 30.

252 Igitur cubus 125, 25, 15 cum cubo 64, 16, 10, totum hoc faciet pyramidis 85 praedictae triplum.

253 Sed per [A:64v] praemissum caput, cubus 125, columna scilicet ^ta cum cubo 64 et 16 format columna ^tam propositam 205.

254 Ergo columna proposita 205 cum 25, ^lo 15, ^lo 10, conficiet praedictum triplum. Verum, ut satis in arithmeticis ostensum est ^li 15 10 conflant ^um 25.

255 Itaque et columna proposita 205 cum duplo ^ti 25, hoc est cum 50 efficiet dictum pyramidis suae ^tae 85 triplum, quod est 255.

256 Quod est propositum.

257 Igitur columna ^ta 2ⁱ ordinis 205 cum 25, 15, 10, hoc est cum duplo 25, quod est 50, faciet 255, triplum videlicet suae pyramidis 85. Quem ad modum proponitur.

258 Omnis columna pentagona 2ⁱ ordinis cum duplo ^ti collateralis ex primo ordine et cum ^lo praecedenti¹²⁹ eiusdem ordinis facit triplum suae pyramidis.

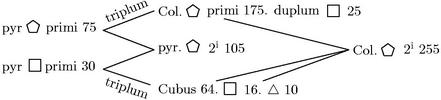
259 Sumatur columna 255 2ⁱ ordinis cum duplo 25, hoc est cum 50, et cum 10 praecedenti consummans iam 315. Aio quod 315 triplus est pyramidis tali columnae respondentis, hoc est pyramidis 105 in 2^o.

260 Nam, per caput antepraemissum, pyramis 105¹³⁰ 2ⁱ ordinis construitur ex pyramide 75 et pyramide 30 in primo ordine.

261 Sed per 3^am primarum propositionum in principio, columna 175 primi ordinis cum duplo 25, hoc est cum 50, facit triplum pyramidis suae 75. Et ut in principio quoque ostensum est, cubus 64, 16, 10, faciunt triplum pyramidis 30, ut in praemissis.

262 Igitur columna 175, duplum 25, cubus 64, 16, 10, hoc totum faciet triplum pyramidis 105 2ⁱ ordinis praedictae.

263 Sed per praemissum caput, columna pentagona 175 cum cubo 64 et 16 format columnam propositam 255.

264 Ergo columna proposita 255 cum duplo 25 et 10 conflabunt praedictum triplum pyramidis suae 105, sicut iam demonstrandum proponitur.

265 Igitur columna 2ⁱ ordinis 255 cum duplo 25 et 10 facit 315, [A:65r] triplum videlicet suae pyramidis 105. Quod est propositum.

266 Cumque 25 cum 10 praecedenti faciat 35 sibi collateralem iam columna pentagona 2ⁱ ordinis una cum ^to et pentagono collateralibus faciet triplum suae pyramidis.

267 Omnis columna hexagona 2ⁱ ordinis cum ^to et ^no collateralibus primi ordinis composita efficit triplum suae pyramidis.

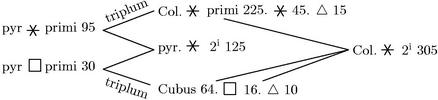
268 Capiatur columna ^na 2ⁱ ordinis quae sit 305, cum 25 et ^no primi 45 consummans iam 375. Aio quod 375 triplus est pyramidis suae 125.

269 Nam, per caput antepraemissum, pyramis 125 2ⁱ ordinis constat ex pyramide 95 primi et ex pyramide 30 praecedenti.

270 Sed, per 5^am praecedentium propositionum, columna ^na primi 225 cum suo 45 et collaterali ^lo 15 efficiebat triplum ^nae pyramidis 95 eiusdem ordinis. Et ut in praemissis, cubus 64, 16, 10, simul sunt triplum pyramidis 30.

271 Igitur columna 225, 45, 15, cubus 64, 16, 10, hoc totum conflabit triplum pyramidis 125 praedictae.

272 Sed per praecedens caput, columna 225 cum cubo 64 et 16 configurant columnam 305 propositam.

273 Ergo columna proposita 305 cum 45, ^lo 15, 10, iuncta conflabit dictum triplum pyramidis 125.

274 Cumque 15 10 faciant quadratum 25, Iam et columna 305 cum 45 et 25 faciet idem triplum pyramidis suae 125, quod est 375. Quod fuit demonstrandum.

275 Igitur columna 305¹³¹ 2ⁱ cum 45 cumque 15, 10, sive cum 25, facit 375, quod est triplum pyramidis 125, sicut proponatur.

276 Cumque, ut constitit, 61 sit aequalis aggregato 45 et 16¹³² primi ordinis appositoque utrobique impari collaterali 9, 61 cum ipso 9 simul aequabitur 45 cum 16 et 9¹³³ impari ipsius 16 ^ti collaterali. Verum 16 cum impari sibi sequenti 9 facit ^tum sequentem 25.

277 Igitur [A:65v] 45 cum 25 fient aequales 61 cum impari 9.

278 Fuerat autem columna 305 cum 45 atque ^to 25, triplum pyramidis suae 125.

279 Ergo et eadem columna 305 cum 61 et impari collaterali 9, dictum suae pyramidis triplum conflabit.

280 Quod nos in alio quaternione Arithmeticae nostrae demonstraveramus.