|
Propositio 98a
1 Quadruplum dicti trianguli, uno intermisso praecedentis imparem, cum sexcuplo pyramidis quadratae centralis immediate dictum imparem praecedentis coniun[C:65r]ctum, conficit duo supplementa, quae singula fiunt ex ductu ipsius imparis in latus secundi quadrati praecedentis; 2 et coniuncta cum quadrato ipsius imparis constituunt gnomonem, qui coniunctus cum secundo quadrato praedicto, construit secundum quadratum sequentem, hoc est, ipsius imparis collateralem.
3 Intelligo secundos quadratos eos qui ex primis in se ductis fiunt: ut 16 est secundus quadratus binarii; 81 secundus quadratus ternarii; et sic deinceps. Itaque exponam primum, dein ostendam propositionem. Exponantur1 ab unitate sex numerorum series, scilicet radices, impares, trianguli primi, pyramides quadratae centrales, quadrati primi, et gnomones secundorum quadratorum, per ordinem continuati. 4 Quibus exaratis, iam in secundo loco, impar est 3; hic autem quadruplum trianguli nullum est: nam retro intermissa unitate, nullus est triangulus; pyramis hunc locum praecedens, est unitas, eius sexcuplus est senarius: qui solus facit hic duo supplementa 3 et 3 quae singula fiunt ex impare huius loci, scilicet ex 3 in latus secundi quadrati praecedentis, scilicet unitatis, hoc est in unitatem. 5 Et coniuncta cum quadrato dicti imparis, scilicet cum novem, conficiunt 15 gnomonem scilicet eiusdem loci, qui applicatus secundo quadrato praedicto, scilicet unitati, construit iam secundum quadratum sequentem, scilicet 16. 6 In tertio autem loco, [C:65v] impar est2 5; quadruplum trianguli, uno retro intermisso, sumpti3, scilicet unitatis, est quatuor; pyramis praecedens est 6, cuius sexcuplum 36 quod cum 4 facit 40 quae sunt duo supplementa, scilicet 20 et 20, quae singula fiunt ex impare dicto, scilicet 5 in 4 latus secundi quadrati praecedentis, qui est 16, et coniuncta cum quadrato dicti imparis, scilicet cum 25, faciunt 65, gnomonem tertium, qui coniunctus cum secundo quadrato praedicto, scilicet 16, conflat iam secundum quadratum sequentem, scilicet 81. 7 In quarto deinde [S:63] loco, impar est 7, quadruplum trianguli uno retro intermisso sumpti4, scilicet ternarii, est 12; pyramis praecedens est 19, cuius sexcuplum 114, quod cum 12 facit 126, quae sunt duo supplementa, scilicet 63 et 63, quae singula fiunt ex impare dicto 7 in 9 latus scilicet secundi quadrati praecedentis, qui fuit 81, et coniuncta cum quadrato dicti5 imparis, scilicet 49, faciunt 175 gnomonem quartum, qui coniunctus secundo quadrato praedicto, scilicet 81, facit 256 secundum quadratum sequentem. 8 Adhuc in quinto loco, impar numerus est 9, quadruplum trianguli non immediate praecedentis, scilicet 6 est 24; 9 pyramis praecedens 44 cuius sexcuplum 264, quod6 cum 24 efficit 2887, quae sunt duo supplementa, scilicet 144 et 1448 quae singula fiunt ex impare dicto, scilicet 9 in 16, latus scilicet quadrati secundi praemissi, qui fuit 256 et coniuncta cum quadrato dicti imparis, scilicet cum 81 faciunt 369 gnomonem iungendum secundo quadrato praedicto, scilicet 2569, ut conflet 625, quadratum secundum quinarii, qui sequitur, positus in praesenti loco. Sic pro sexto, septimo, et sequentibus locis in infinitum fit similiter seriatim procreando secundos radicum quadratos. 10 Sed demonstrandum quo pacto in singulis locis quadruplum trianguli, ex tertio retrorsum loco sumpti, cum sexcuplo pyramidis quadratae praecedentis coniunctum, facit dicta duo supplementa, sive (quod idem est) quod duplum talis trianguli cum triplo talis pyramidis coniunctum, facit unum tale supplementum, quod (ut dictum est) fit ex impare ipsius loci in latus secundi quadrati praecedentis; et proinde duo talia supplementa coniuncta cum quadrato dicti imparis, componunt gnomonem, qui iunctus cum secundo quadrato praedicto conficit secundum quadratum sequentem, imparique collateralem.
|
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Radices | |
1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | Impares | |
1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | 45 | 55 | Trianguli primi | |
1 | 6 | 19 | 44 | 85 | 146 | 231 | 344 | 489 | 670 | Pyramides quadratae
centrales | |
1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | Quadrati primi | |
1 | 15 | 65 | 175 | 369 | 671 | 1105 | 1695 | 2465 | 3439 | Gnomones
2i |
[S:64] [C:66v] 11 Verum in primo post unitatem loco, qui10 secundus appellatur, in quo (ut dixi) quadruplum11 trianguli12 nullum est, liquet quod triplum pyramidis praecedentis, scilicet 3, facit tale supplementum, quod scilicet fit ex impare huius loci, qui ternarius est, in latus secundi quadrati praecedentis, scilicet in unitatem; 12 et idcirco per quartam13 secundi Euclidis, duo huiusmodi supplementa coniuncta cum quadrato dicti imparis, scilicet 9, conficiunt 15 gnomonem scilicet eiusdem loci, qui appositus secundo quadrato praedicto, scilicet unitati, construit secundum quadratum sequentem, scilicet 16 collateralem ipsius imparis, cuius quidem latus est quadratus ipse14 primus15, scilicet 4 quoniam tale latus ex aggregatione constat unitatis et sequentis imparis, per decimam quintam huius libri. 13 In tertio loco id ipsum quoque ostendemus; in quo impar est 5, quadruplum trianguli 4, et pyramidis sexcuplum 36, et ideo trianguli duplum 2, pyramidis triplum 18. Quare hic ostendendum est quod 2 cum 18 faciunt 20 supplementum quod fit ex impare huius loci, scilicet 5, in latus secundi quadrati praecedentis, hoc est in 4 quod sic patet. 14 Nam columna quadrata centralis praecedentis loci, scilicet 10, cum duplo quadrati primi eiusdem loci, scilicet cum 8, per octogesimam huius, efficit triplum pyramidis eiusdem loci, quae16 fuit 6, hoc est 18. Cui numero [C:67r] addo 2 parte altera longiorem eiusdem loci, et fiunt 20. 15 Cumque 10 columna dicta17 fiat ex radice eiusdem loci, scilicet 2 in quadratum centralem collateralem, scilicet in 5 atque ipse 5 constet ex quadrato primo collaterali et praecedenti, hoc est, ex 4 et 1, iam ipse 10 fit ex 2 in 4 et ex 2 in 1. <At 2 parte altera longior, fit ex 2 in 1. Ergo 2 qui fit ex 2 in 118> coniunctus cum secundo parte altera longiore, hoc est totus 4, fiet19 ex 2 in 2 quod est aggregatum ex 1 et 1. 16 Sic habemus tria producta, scilicet 8 ex 2 in 4, quod fuit duplum quadrati cum columna coniunctum, item 8 ex20 2 in 4 atque 4 ex 2 in 2, integrantia21 totum numerum 20; cumque ex toto numero 20 ipse octonarius contineat bis 4 et rursum 8 bis 4, demonstrandum est quod reliquum, scilicet 4, contineat semel ipsum 4 ut totus 20 contineat quinquies, scilicet secundum numerum imparem huius loci22, ipsum quatuor. 17 Quod iam ratione comprobatur: quoniam scilicet 4 fit ex radice secundi loci, hoc est, ex 2 in parte altera longiorem23 eiusdem loci, scilicet in 2. Et perinde factus adaequatur quadrato collaterali, scilicet 4, sicut et radix aequalis est ipsi parte altera longiori. 18 Produ [S:65] citur itaque in hoc loco 20, supplementum ex 5 in 4; et perinde24 duo talia supplementa, scilicet 20 et 20, coniuncta cum 25 quod est quadratum ipsius 5 imparis, fa[C:67v]ciunt gnomonem 65, qui coniunctus cum quadrato ipsius 4 scilicet cum 16, quadrato secundo praecedentis loci, scilicet secundi, constituit sequentem quadratum secundum, collateralem, scilicet huic loco tertio, qui est 81. 19 Nam per quartam secundi Euclidis, supplementa duo ex lateribus quadratorum duorum producta, una cum ipsis quadratis, componunt quadratum, cuius latus constat ex lateribus quadratorum componentium. Sed unum laterum talium fuit quadratus numerus, scilicet 4 et alterum fuit sequens impar, scilicet 5. 20 Ergo et compositus ex illis, per decimam quintam huius libri, erit quadratus sequens, scilicet 9, latus scilicet totalis quadrati; et perinde totalis quadratus erit quadratus secundus ternarii, scilicet 81 qui ex 9 in se fit. In quarto etiam loco nunc demonstrationem repetemus: in quo impar est 7, quadruplum trianguli est 12, sexcuplum pyramidis 114; et ideo <duplum25> trianguli 6, triplum pyramidis 57. 21 Quare hic ostendendum est quod26 6 cum 57 efficit 63 supplementum, quod fit ex impare huius loci, scilicet 7 in latus secundi quadrati praecedentis, hoc est in 9, quod sic patet. Nam columna quadrata centralis praecedentis loci, scilicet 39, cum27 duplo quadrati primi eiusdem loci, scilicet cum 18, efficit, per octogesimam huius, [C:68r] triplum pyramidis eiusdem loci, hoc est 57. 22 Cui numero adiicio 6 parte altera longiorem eiusdem loci, et fiunt 63. Cumque 39 columna dicta28 fiat29 ex radice eiusdem loci, scilicet 3, in quadratum centralem collateralem, scilicet in 13, atque ipse 13 constet ex duobus quadratis primis, scilicet collaterali et praecedenti, hoc est, ex 9 et 4, iam ipse 39 fiet ex 3 in 4 et ex 3 in 9. 23 At ipse 6 parte altera longior, fit ex 3 in 2. Ergo 12 qui fit ex 3 in 4 coniunctus cum 6 parte altera longiore30, scilicet 18, fiet ex 3 in 6 quod est aggregatum ex 4 et 2. Sic habemus tria producta, scilicet 18 ex 2 in 9 quod fuit duplum quadrati cum columna coniunctum, item 27 ex31 3 in 9, atque 18 ex 3 in 6 integrantia32 totum 63. 24 Cumque ex toto numero 63, ipse 18 contineat bis 9 et ipse 27 contineat ter 9, demonstrandum est quod residuum scilicet 18 continet bis 9 ut videlicet totus 63 concludatur continere septies ipsum 9, secundum imparem scilicet huius loci, qui septenarius est. Quod et ratione confirmatur.
[S:66] 25 Quoniam 18 producitur ex radice tertii loci scilicet 3 in 6 parte altera longiorem eiusdem loci, et perinde33 productus duplus est ad quadratum eiusdem loci, scilicet ad 9, quotuplus est parte altera longior ipsius radicis. 26 Producitur itaque in hoc loco supplementum 63 ex 7 in 934. Et perinde35 duo talia supplementa 63 et 63 coniuncta [C:68v] cum 49 quadrato ipsius imparis, faciunt gnomonem 175; qui coniunctus cum quadrato ipsius 9 scilicet cum 81 quadrato secundo praecedentis loci, scilicet tertii, componunt quadratum secundum sequentem scilicet 256 collateralem, hoc est, huius quarti loci. 27 Nam, per quartam secundi Euclidis, duo quadrata et duo supplementa ex lateribus quadratorum producta36 pariter accepta, conficiunt quadratum totalem, cuius latus est aggregatum ex lateribus quadratorum partialium. 28 Cumque unum horum laterum fuerit iam quadratus numerus, scilicet 9, et reliquum impar numerus sequens scilicet 7, iam aggregatum ex ipsis, totalis scilicet quadrati latus, erit, per decimam quintam huius, erit quadratus sequens, scilicet 16, latus scilicet totalis quadrati. Unde totalis quadratus erit quadratus secundus, scilicet 256 qui fit ex 16 in se. 29 Lubet et in quinto loco demum propositum demonstrare. 30 In quo quidem impar est 9, quadruplum trianguli saepe dicti 24, sexcuplum pyramidis 264; et ideo duplum trianguli 12, triplum pyramidis 132. Quare hic ostendendum quod 12 cum 132 efficit 144 supplementum quod fit ex impare huius [C:69r] loci, scilicet 9, in latus secundi quadrati praecedentis, scilicet in 16. 31 Quod sic potest concludi: nam per octogesimam huius, columna quadrata centralis praecedentis loci, scilicet 100, cum duplo quadrati primi eiusdem loci, scilicet cum 32, efficit triplum pyramidis suae eiusdem loci, quae fuit 44, hoc est 132, cui numero addo ipsum 12 parte altera longiorem, et conficio 144; cumque 100 columna praedicta fiat ex radice eiusdem loci, scilicet 4 in quadratum centralem collateralem, scilicet in 25 atque ipse 25 constet ex duobus quadratis primis, scilicet collaterali et praecedenti, hoc est, ex 16 et 9, iam37 ipse 10038 fiet ex39 4 in 16 et ex 4 in 9. 32 At ipse 12 parte altera longior fit ex 4 in 3. Ergo 36 qui fit ex 4 in 9, coniunctus cum 12, scilicet totus 48, fiet ex 4 in 1240 quod est aggregatum ex 9 et 3. Sic habemus tria producta: scilicet 32 ex 2 in 16, quod fuit duplum quadrati cum columna coniunctum, 64 ex 4 in 16 atque 48 ex 4 in 12 integrantia totum 144. 33 Cumque ex toto numero 144 ipse 32 contineat bis 16 et ipse 64 quater [S:67] 16, demonstrandum restat quod residuum scilicet 48 contineat ter41 16 ut scilicet totus 144 comprehendat novies 16, iuxta imparem huius loci, scilicet 9; quod, sicut prius, fa[C:69v]cile ostenditur. 34 Quoniam 48 producitur ex radice quarti loci, scilicet 4 in 12 parte altera longiorem eiusdem loci, et idcirco productus est triplus ad quadratum collateralem, scilicet ad 16, quotuplus42 est parte altera longior ipsius radicis. 35 Producitur itaque in hoc loco supplementum 144 ex 9 in 16 et ideo duo talia supplementa, scilicet 144 et 144, coniuncta cum 81 quadrato ipsius imparis 9 faciunt43 gnomonem 369 qui coniunctus cum quadrato ipsius 16 scilicet cum 256 quadrato secundo praecedentis loci, scilicet quarti, componit sequentem quadratum secundum, scilicet 625, huius quinti loci. 36 Nam per quartam secundi Euclidis, duo quadrata et duo supplementa ex lateribus quadratorum producta pariter accepta, conficiunt quadratum totalem, cuius latus est aggregatum ex lateribus quadratorum partialium. 37 Cumque unum horum laterum fuerit quadratus numerus, scilicet 16 et reliquum impar numerus sequens, scilicet 9, iam per decimam quintam huius, aggregatus ex44 ipsis, totalis scilicet quadrati latus, erit numerus quadratus, scilicet 25. Unde totale quadratum erit quadratus secundus, scilicet 625 qui fit ex 25 quadrato huius quinti loci in se multiplicato. 38 Similiter in sexto, septimo, octavo et caeteris deinceps locis45 in infinitum [C:70r] continuabitur haec demonstratio. Namque in sexto loco argues tria producta integrantia supplementum, continere praecedentem quadratum undecies; in septimo loco tredecies; in octavo quindecies; in nono septemdecies, in decimo undevigesies et sic deinceps per impares sequentes, ut hic46 in margine notavi, quo constet propositum.
2  | 5 |  | 10 | 2  | 4 |  | 8 | | 1 |  | 2 | | 1 |  | 2 |
2  | 4 |  | 8
|
3  | 13 |  | 39 | 3  | 9 |  | 27 | | 4 |  | 12 | | 2 |  | 6 |
2  | 9 |  | 18
|
4  | 25 |  | 100 | 4  | 16 |  | 54 | | 9 |  | 36 | | 3 |  | 12 |
2  | 6 |  | 32
|
|
locus | | 2us | 2  bis bis |  | 1  semel semel | ter  1 1 | 0  nihil nihil |
| 3
|
| 3us | 8  bis bis | 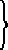 | 8  bis bis | quinquies  4 4 | 4  semel semel |
| 20
|
| 4us | 18  bis bis | 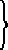 | 27  ter ter | septies  9 9 | 18  bis bis |
| 53
|
| 5us | 32  bis bis | 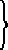 | 64  quater quater | novies  16 16 | 48  ter ter |
| 144
|
| 6us | 50  bis bis | 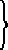 | 125  quinquies quinquies | undecies  25 25 | 100  quater quater |
| 175
|
| 7us | 72  bis bis |  | 216  sexies sexies | tredecies  36 36 | 180  quinquies quinquies |
| 468
|
| 8us | 98  bis bis |  | 343  septies septies | quindecies  49 49 | 294  sexies sexies |
| 735
|
| 9us | 128  bis bis |  | 512  octies octies | 17ties  64 64 | 448  septies septies |
| 1088
|
| 10us | 162  bis bis |  | 729  novies novies | 19ties  81 81 | 648  octies octies |
| 1539
|
| 11us | 200  bis bis |  | 1000  decies decies | 21ties  100 100 | 900  novies novies |
| 2100
|
|
Et sic deinceps in infinitum | |
Et productum medium semperest | |
cubus praecedentis loci.
|
|
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Radices | |
1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | Impares | |
1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | 45 | 55 | Trianguli primi | |
1 | 6 | 19 | 44 | 85 | 146 | 231 | 344 | 489 | 670 | Pyramides
quadratae centrales | |
1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | Quadrati primi | |
1 | 15 | 65 | 175 | 369 | 671 | 1105 | 1695 | 2465 | 3439 | Gnomones |
|