PROPOSITIO XX.
Si recta spiram primae revolutionis tangat, non quidem in eius termino; et a puncto contactus ad initium spirae recta ducatur; ipsoque initio posito centro ad spatium ductae circulus describatur; item per perpendicularis ad ductam excitetur ab initio spirae: excitata cum tangente concurret; et ipsa inter initium, et concursum recepta aequalis erit peripheriae circuli descripti ab exordio dictae revolutionis ad contactum usque, secundum revolutionis ordinem computatae.
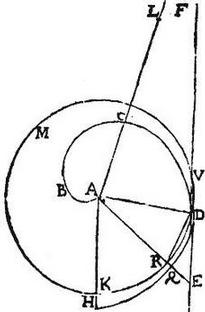
Sit spira primae revolutionis ABCDH cuius initium A, linea revolutionis initium AH, tangens spiram sit recta EDF, punctum contactus D, connexaque AD ipsi perpendicularis ducatur AF; cumque ADF angulus acutus sit per 16. huius, ipsae AF, DF concurrent, utpote ad F. Descriptoque super centrum A ad spatium AD circulo DMK. Ostendendum est quod linea AF aequalis est peripheriae circulari KMD nam secus, erit aut maior, aut minor. Sit primum maior AF, quam peripheria KMD; et hinc ponatur AL brevior quidem, quam AF, maior autem, quam peripheria KMD. Eritque ratio DA, ad AL maior quam semissis DV chordae ad perpendicularem sibi eductam a puncto A; quippe quae est sicut DA ad AF, propter similitudinem triangulorum: igitur per 5. huius, potest educi linea ARE, secans circulum apud R, et tangentem apud E, et spiralem apud Q; ita ut RE ad DR chordam sit, sicut DA ad AL; hoc est AR ad AL. Eritque permutatim ER ad RA, sicut chorda DR ad AL: sed ratio chordae DR, ad AL minor est, quam arcus DR ad peripheriam KMD; quandoquidem DR chorda brevior est arcu DR; et AL maior, quam peripheria KMD. Ergo ratio ER ad RA minor est, quam arcus DR ad peripheriam KMD; et coniunctim ratio EA, ad AR minor quam peripheriae RDMK ad peripheriam KMD circuli; sed per 14. huius, sicut KMDR peripheria ad KMD peripheriam, sic AQ ad AD, quae ad spiralem ambitum terminantur. Igitur ratio EA ad AR minor, quam AQ ad AD; et permutatim [S:214] ratio EA ad AQ minor, quam AR ad AD; sed AR, AD aequales sunt. Ergo AQ longior est, quam AE pars toto; quod est impossibile. Non est ergo maior AF arcu KMD. Et similiter, sicut in 18 fecimus, ostendemus, quod nec minor. Unde superest ut sit aequalis, sicut demonstrandum proponitur.
SCHOLIUM.
Quod si recta spiram secundae revolutionis tangat non in eius termino; et caetera ut dudum disponantur: recepta inter initium spirae, et concursum aequalis erit peripheriae totius circuli per contactum descripti, et insuper arcui ab exordio spirae ad contactum usque continuato secundum ordinem revolutionis. Sed et in spiris tertiae, quartae, et quotecumque revolutionis, talia recepta multiplex erit ad ambitum dicti circuli secundum numerum unitate minorem numero revolutionum; et insuper comprehendet peripheriam ab initio ad contactum per ordinem revolutionis deductam; quae omnia eodem modo demonstrantur.