PROPOSITIO IX.
Si in circulo descripti polygonii aequilateri dimidium ad terminos diametri terminatum diametro stante, donec ad locum suum redeat, circumducatur: descripti solidi tota superficies aequalis erit ei, quod fit ex ductu peripheriae continentis polygonium in lineam, quae cum diametro eiusdem circuli, et latere polygonii in ipso circulo constituit trigonum rectangulum.
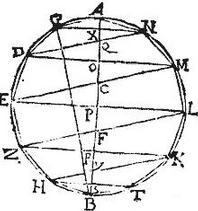
Intra circulum AB, cuius diameter AB sit descriptum aequilaterum polygonium, quodvis ut puta dodecagonum, cuius anguli sint apud puncta A, G, D, E, Z, H, B, T K, L, M, N, et ducantur lineae GN, DM, EL, ZK, HT secantes orthogonaliter diametrum AB apud puncta XOPRS. Item lineae DN EM, ZL, HK, secantes dictum diametrum apud puncta YFCQ. Item recta BG faciens cum GA latus rectum angulum per 29.3. et circumducto semipolygonio AEB super axem AB completo ambitu describatur solidum tornatile conicarum superficierum, quemadmodum in praecedenti. Aio, quod huiusmodi solidi tota superficies, quae scilicet aggregatum est conicarum superficierum a lateribus semipolygonii descriptarum, aequalis est ei, quod fit ex ductu lineae BG in peripheriam circuli AB. Nam per praecedentem , quod fit ex AG in omnes peripherias descriptas ab angulis G, D, E, Z, H aequum est toti superficiei solidi a semipolygonio descripti, quam demonstrationem, si placet, sic repete.
|
Et hoc per 7. praemissam et 2. Quare per 1.2. Elementorum tota superficies solidi a semipolygonio descripti, aequalis est ei, quod fit ex latere AG in omnes peripherias, quarum diametri GN, DM, EL, ZK, HT. Sed triangula GAX, NQX, DQO, MCO, [S:51] ECP, LFP, ZFR, KRY, HXS, TBS sunt similia triangulo BGA quoniam scilicet sunt orthogonia, et anguli assumentes aequales arcus, sunt aequales per 26.3. quare, et reliqui aequales.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Quare per 13.5. sic ut BG ad GA, sic aggregatum GN, DM, EL, ZK, HT ad totam AB, et ideo per corollarium 6. huius, sicut BG ad GA, sic peripheria, cuius diameter est aggregatum ex GN, DM, EL, ZK, HT, ad peripheriam, cuius diameter AB. Sed peripheria, cuius diameter est aggregatum ex GN, DM, EL, ZK, HT, per corollarium 6. huius, aequalis est aggregato peripheriarum, quarum diametri GN, DM, EL, ZK, HT. Igitur sicut BG ad GA, sic aggregatum peripheriarum quarum diametri GN, DM, EL, ZK, HT, ad peripheriam, cuius diameter AB. Quare per 15. sexti Elementorum, quod fit ex BG in peripheriam, cuius diameter AB, aequum est ei, quod fit ex GA in aggregatum peripheriarum, quarum diametri GN, DM, EL, ZK, HT. Sed per praecedentem, quod fit ex GA in aggregatum peripheriarum, quarum diametri GN, DM, EL, ZK, HT, aequale est superficiei solidi a semipolygonio AEB descripti: ergo quod fit ex BG in peripheriam, cuius diameter AB aequale, est superficiei solidi a semipolygonio AEB descripti; et hoc erat demonstrandum.
COROLLARIUM I.
Unde et quod fit ex diametro AB in peripheriam circuli, cuius diameter est BG. Aequale erit eiusdem solidi tornatilis superficiei, quod quidem sequitur ex praesenti, et ex tertio corollario primae. Item circulus, cuius semidiameter est media proportionalis inter ipsas lineas AB, BG aequalis est superficiei memorati solidi tornatilis: quod sequitur ex ultimo corollario primae.
COROLLARIUM II.
Hinc manifestum est quod superficies solidi a semipolygonio AEB descripti aequalis est cylindricae superficiei, cuius axis est linea BG, et basis circulus AB; namque per 4. huius, cylindrica superficies aequalis est ei, quod ex axe in peripheriam basis. [S:52]
COROLLARIUM III.
Item quod fit ex perpendiculari a centro circuli ad latus polygonii in peripheriam circuli continentis polygonium, dimidium est totius superficiei solidi a semipolygonio super diametrum semel revoluto descripti. Nam perpendicularis, quae a centro P ad latus AG dimidium est ipsius BG. Sicut AP dimidium ipsius AB. Itaque quod ex dicta perpendiculari in peripheriam AB dimidium est eius, quod ex BG in peripheriam AB: et ideo dimidium superficiei praedicti solidi a semipolygonio descripti.