PROPOSITIO X.
Sphaerae superficies aequalis est rectangulo, quod fit ex diametro sphaerae in peripheriam maximi sui circuli.
Sit circulus ABGD, cuius centrum E diameter AG, et circumducto semel altero semicirculorum, ut puta semicirculo ABG stante diametro AG, describatur sphaera ABG. Aio quod superficies sphaerae ABG aequalis est ei, quod fit ex diametro AG in peripheriam circuli ABG; nam si quod fit ex AG in peripheriam circuli ABG non est aequale superficiei sphaerae ABG, erit aequale superficiei sphaerae alicuius maioris, vel minoris sphaera ABG.
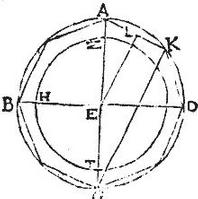
Sit ergo primum aequale superficiei sphaerae ZHT minoris ipsa sphaera ABG, et cum ea concentricae, cuius diameter ZT, et quam circa diametrum ZT revolutus describit semicirculus ZHT, et per 13.12. inscribatur circulo ABG polygonium aequalium laterum minime tangentium circulum ZHT, quod sit polygonium ABGD, cuius laterum unum sit AK, et connectatur GK, ac polygonii dimidio circa diametrum AG circumducto, describatur solidum tornatile conicarum superficierum iam minime tangentium sphaeram ZHT, eritque per praecedentem, quod fit ex GK in peripheriam ABG circuli aequum superficiei universae solidi ABG a semipolygonio descripti: sed quod fit ex diametro AG in peripheriam circuli ABG maius est eo, quod ex GK in peripheriam eandem: ergo quod fit ex diametro AG in peripheriam circuli ABG, et ideo ipsa sphaerae ZHT superficies, maior erit solidi a semipolygonio ABG descripti superficie: inclusa includente, quod est impossibile. Vel sic quoniam quod fit ex AG diametro in peripheriam ABG circuli maius est solidi a semipolygonio ABG descripti superficie, et haec maior superficie sphaerae ZHT inclusae: ideo quod fit ex AG diametro in peripheriam ABG circuli, maius est ipsa sphaerae ZHT superficie: non est ergo ei aequalis sicut supponebatur. Sit deinde quod fit ex AG in peripheriam circuli ABG aequale superficiei sphaerae maioris ipsa sphaera ABG, sed brevitatis causa, sit proposita sphaera ZHT. Aio quod id quod fit ex diametro ZT in peripheriam circuli ZHT non erit aequale superficiei alicuius sphaerae maioris sphaera ZHT. Nam si possibile est, sit aequale superficiei sphaerae ABG ipsi ZHT concentricae, et quam circa diametrum AG describit semicirculus ABG, et inscribatur, ut prius, circulo ABG polygonium aequalium laterum non tangentium circulum ZHT cuius unum laterum fit AK, et ducetur GK, et EL perpendicularis ad AK, et circumducto semipolygonio ABG super diametrum AG describatur solidum tornatile conicarum superficierum, [S:53] iam minime tangentium sphaeram ZHT. Est autem GK dupla ipsius EL, sicut AG dupla ipsius AE: sed ZT dupla ipsius ZE minor ipsa EL: ergo GK maior quam ZT. Quare quod fit ex GK in peripheriam circuli ABG maius est eo, quod fit ex diametro ZT in peripheriam circuli ZHT. Verum quod fit ex GK in peripheriam circuli ABG, per praecedentem aequale est superficiei solidi a semipolygonio ABG descripti: quod autem fit ex diametro ZT in peripheriam circuli ZHT aequum est (per hypothesim) superficiei sphaerae ABG. Igitur superficies solidi a semipolygonio ABG descripti maior est superficie sphaerae ABG; inclusa includente, quod est impossibile. Non est ergo quod fit ex ZT diametrum in peripheriam ZHT aequale superficiei alicuius sphaerae maioris sphaera ZHT. Similiter ostendam quod id quod fit ex AG diametrum in peripheriam circuli ABG non est aequale superficiei sphaerae alicuius maioris sphaera ABG; sed nec minoris, ut fuit ostensum. Superest ergo ut id, quod fit ex diametro AG in peripheriam ABG aequale sit superficiei sphaerae ABG. Quod erat demonstrandum.
COROLLARIUM.
Manifestum est ergo quod sphaerae superficies aequalis est circulo, cuius semidiameter aequalis est diametro sphaerae; nam area talis circuli per 4. de dimensione circuli producitur ex suo semidiametro, quae est diameter sphaerae in dimidium suae peripheriae, quae per sextam huius, aequalis est peripheriae circuli, maximi in sphaera.