[S:153]

PROPOSITIO XXVI

Si recta aequidistans basi conicae sectionis, quae parabolae dicitur ducatur; sectio tota ad abscissam portionem erit sicut cubus basis ad cubum ductae aequidistantis.

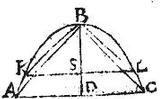
Sit parabole ABC, cuius diameter BD, basis AC, cui aequidistans ducatur KL secans ipsam BD apud S: dico quod sectio ABC ad portionem KBL est sicut cubus, qui ex AC ad cubum, qui ex KL: nam cum diameter sectionis sit BD, linea tangens sectionem apud B aequidistabit per 5.2. conicorum elementorum, ipsi AC, et perinde ipsi KL: quare per 46. primi conicorum, KL bifariam secatur apud S. Demonstrandum est igitur quod sectio ABC ad sectionem BKL est sicut cubus, qui ex AD ad cubum, qui ex KS. Sic; coniungantur AB, BC, et KB, BL: et quoniam ratio triangulorum componitur ex basium, et altitudinum rationibus; ideo ratio trianguli ABC ad triangulum KBL componetur ex rationibus duabus, scilicet ex ratione AD ad KS, et ex ratione DB ad BS: sed per 20. primi conicorum elementorum, sicut BD ad BS, sic quadratum AD ad quadratum KS. Igitur ratio trianguli ABC ad triangulum KBL componetur ex ratione AD ad KS, et ex ratione quadrati AD ad quadratum KS: dupla est autem ratio quadrati AD ad quadratum KS rationis AD ad KS: ergo ratio trianguli ABC ad triangulum KBL tripla erit rationis AD ad KS. Verum ratio cubi, qui ex AD ad cubum qui ex KS tripla est rationis AD ad KS. Igitur sicut cubus, qui ex AD ad cubum, qui ex KS, sic triangulum ABC ad triangulum KBL: sed per demonstrata de quadratura parabolae, sicut est triangulum ABC ad triangulum KBL, sic sectio ABC ad sectionem KBL, (omnis enim parabola sesquitertia est sui trianguli) ergo sicut sectio ABC ad sectionem KBL, sic cubus, qui ex AD ad cubum, qui ex KS: quod iam erat demonstrandum.