PROPOSITIO XV.
Si intra sectionem vocatam parabolen triangulum inscribatur habens eandem basim cum sectione, et verticem eundem, et rursum in susceptis periferiae proportionibus triangula inscribantur easdem cum portionibus bases, et vertices habentia; itemque in relictis portionibus eadem triangulorum inscriptio continuetur; figura in sectione hoc modo inscripta, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , hoc est perspecte inscribi dicitur ab Archimede.
, hoc est perspecte inscribi dicitur ab Archimede.
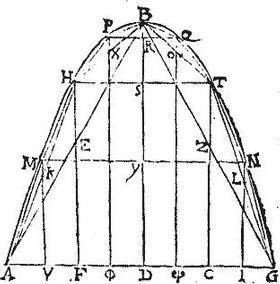
Manifestum est autem, quod in huiusmodi figura lineae rectae, quae iungunt angulos proximos a praecipuo vertice, et binos per ordinem hinc inde sequentes, aequidistabunt basi paraboles, et crescent a prima secundum crementum aequale primae, et singulae per aequalia dividentur a praecipua diametro, et vicissim ipsae diametrum secabunt, itaut ab ipsis ad verticem receptae portiones diametri sint in proportione numerorum imparium per ordinem sumptorum ab unitate; unde diameter sectionis est et axis figurae inscriptae.
Sit conica sectio vocata parabole ABG basim habens rectam lineam AG atque diametrum BD, in qua inscribatur triangulum ABG: rursumque divisis per medium rectis AB, BG in punctis E, Z ducantur aequidistantes ipsi BD lineae utrinque ad periferiam, et basim productae HEF, TZC: tales enim lineae diametri erunt per 46. primi conicorum elementorum; et per 5. secundi eorumdem, lineae tangentes sectionem apud H, T puncta aequidictabunt ipsis AB, BG, et ideo HT puncta vertices erunt relictarum sectionum AHB, BTG: in his itaque portionibus inscribantur rursus triangula AHB, BTG, et similiter divisis per medium rectis AH, HB, BT, TG in punctis K, X, O, L: et per talia puncta productis ad aequidistantiam ipsius BD praecipuae diametri tertiis diametris utrinque ad peripheriam, et basim MKV, PX![]() , QO
, QO![]() , NLI; similiter atque tertio in relictis portionibus quatuor totidem triangula inscribantur AMH, HPB, BQT, TNG: itaque figura rectilinea ex [S:145] novem lateribus AMHPBQTNG intra peripheriam paraboles ABG inscripta dicitur ab Archimede perspecte, sive cognite inscripta.
, NLI; similiter atque tertio in relictis portionibus quatuor totidem triangula inscribantur AMH, HPB, BQT, TNG: itaque figura rectilinea ex [S:145] novem lateribus AMHPBQTNG intra peripheriam paraboles ABG inscripta dicitur ab Archimede perspecte, sive cognite inscripta.
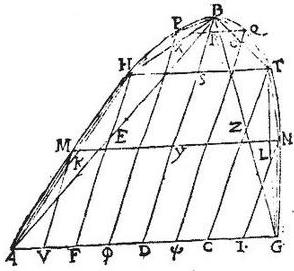
Similiter pentagonum AHBTG figura note inscripta in parabola vocatur, et omnis alia eodem ordine continuato descripta: divisis scilicet deinceps chordis singulis bifariam; ductisque per puncta divisionum diametris, triangulisque per relictas portiones distributis. Demonstrandum est igitur, quod coniunctae lineae PQ, HT, MN, aequidistabunt ipsi basi AG; quodque HT est maior quam PQ in quantitate PQ, et sic deinceps; quodque in punctis R, S,Y bifariam secantur; quodque portiones diametri BD ipsae scilicet BR, RS, SY, YD, sunt ad invicem in proportione imparium numerorum ab unitate ordinatorum. Sic, quoniam per hypothesim HX aequalis XB, aequidistant autem P![]() BD; ideo et F
BD; ideo et F![]() ,
, ![]() D aequales, quando iisdem interponuntur aequidistantibus, quibus ipsae HX, XB: nec non et ipsae D
D aequales, quando iisdem interponuntur aequidistantibus, quibus ipsae HX, XB: nec non et ipsae D![]() ,
, ![]() C aequales, quippe quae iisdem intersunt aequidistantibus, quibus ipsae BO, OT, per hypothesim aequales. Item quoniam per hypothesim AK, KH aequales, et TL, LG aequales, iam cum simili ratione ipsae AV, VF inter se aequales, et ipsae CI, IG inter se aequales erunt; adhuc quoniam per hypothesim aequales sunt AE, EB. Item, et aequales BZ, ZG; ideo AF, FD aequales invicem; et DC, CG aequales invicem erunt: cum igitur AG secetur apud D in dimidia, apud F, C in quartas; secabitur iam apud reliqua puncta V
C aequales, quippe quae iisdem intersunt aequidistantibus, quibus ipsae BO, OT, per hypothesim aequales. Item quoniam per hypothesim AK, KH aequales, et TL, LG aequales, iam cum simili ratione ipsae AV, VF inter se aequales, et ipsae CI, IG inter se aequales erunt; adhuc quoniam per hypothesim aequales sunt AE, EB. Item, et aequales BZ, ZG; ideo AF, FD aequales invicem; et DC, CG aequales invicem erunt: cum igitur AG secetur apud D in dimidia, apud F, C in quartas; secabitur iam apud reliqua puncta V![]() ,
, ![]() I in octavas, et perinde octo portiones AV, VF, F
I in octavas, et perinde octo portiones AV, VF, F![]() ,
, ![]() D, D
D, D![]() ,
, ![]() C, CI, IG invicem aequales erunt: quoniam ergo
C, CI, IG invicem aequales erunt: quoniam ergo ![]() D, D
D, D![]() aequales: ideo et PR, RQ iisdem aequidistantibus interiectae aequales erunt; et similiter quoniam FD, DC aequales, ideo et HS, ST aequales; ideo, et MY, YN aequales erunt. Itaque PQ, HT, MN per aequa secantur in punctis R, S, Y: quamobrem diameter cum sit BD linea tangens sectionem apud B, aequidistabit unicuique ipsarum PQ, HT, MN, AG per 5. secundi Conicorum elementorum, et idcirco ipsae PQ, HT, MN, AG aequidistantes erunt. Item sicut AG quadrupla est ad
aequales: ideo et PR, RQ iisdem aequidistantibus interiectae aequales erunt; et similiter quoniam FD, DC aequales, ideo et HS, ST aequales; ideo, et MY, YN aequales erunt. Itaque PQ, HT, MN per aequa secantur in punctis R, S, Y: quamobrem diameter cum sit BD linea tangens sectionem apud B, aequidistabit unicuique ipsarum PQ, HT, MN, AG per 5. secundi Conicorum elementorum, et idcirco ipsae PQ, HT, MN, AG aequidistantes erunt. Item sicut AG quadrupla est ad ![]()
![]() , ita, et quadrupla ad PQ, et sicut VI tripla ad
, ita, et quadrupla ad PQ, et sicut VI tripla ad ![]()
![]() , ita et MN tripla ad PQ, et sicut FC dupla ad
, ita et MN tripla ad PQ, et sicut FC dupla ad ![]()
![]() , sic HT dupla ad PQ. Itaque PQ, HT, MN, AG, sunt ad invicem in proportione numerorum ab unitate, et per unitatem crescentium; sed per 20. primi conicorum elementorum, sicut sunt ad invicem quadrata linearum PQ, HT, MN, AG; sic sunt in proportione lineae BR, BS, BY, BD; igitur lineae BR, BS, BY, BD sunt in proportione quadratorum numerorum, qui fiunt a numeris ab unitate naturali ordine crescentibus. Et perinde talium linearum differentiae scilicet ipsae portiones BR, RS, SY, YD, sunt in proportione illa, in qua talium quadratorum numerorum differentiae: sed quadratorum ab unitate dispositorum differentiae sunt impares numeri ab unitate ordinati, sicut ostendit Iordanus in Arithmeticis: ergo, et portiones BR, RS, SY, YD sunt in proportione imparium numerorum ab unitate ordinatorum; et haec fuerant in propositione demonstranda. [S:146]
, sic HT dupla ad PQ. Itaque PQ, HT, MN, AG, sunt ad invicem in proportione numerorum ab unitate, et per unitatem crescentium; sed per 20. primi conicorum elementorum, sicut sunt ad invicem quadrata linearum PQ, HT, MN, AG; sic sunt in proportione lineae BR, BS, BY, BD; igitur lineae BR, BS, BY, BD sunt in proportione quadratorum numerorum, qui fiunt a numeris ab unitate naturali ordine crescentibus. Et perinde talium linearum differentiae scilicet ipsae portiones BR, RS, SY, YD, sunt in proportione illa, in qua talium quadratorum numerorum differentiae: sed quadratorum ab unitate dispositorum differentiae sunt impares numeri ab unitate ordinati, sicut ostendit Iordanus in Arithmeticis: ergo, et portiones BR, RS, SY, YD sunt in proportione imparium numerorum ab unitate ordinatorum; et haec fuerant in propositione demonstranda. [S:146]
SCHOLIUM.
Et notandum, quod lineae AB, HT, P![]() secant se super uno puncto, super quo quidem ipsae EB, HS singulae per medium secantur. Item lineae BG, HT, Q
secant se super uno puncto, super quo quidem ipsae EB, HS singulae per medium secantur. Item lineae BG, HT, Q![]() super unico puncto se invicem secant, super quo ipsae BZ, ST se singulae per aequalia dispescunt. Item attendendum, quod in praesenti demonstratione utrum BD diameter praecipua sit axis in sectione, hoc est ad rectos ipsis PQ, HT, MN, AG ordinate ductis, an non sit axis, hoc est non ad rectos ipsis ordinate ductis, non refert: nam propositiones conicorum adductae ad omnem diametrum faciunt.
super unico puncto se invicem secant, super quo ipsae BZ, ST se singulae per aequalia dispescunt. Item attendendum, quod in praesenti demonstratione utrum BD diameter praecipua sit axis in sectione, hoc est ad rectos ipsis PQ, HT, MN, AG ordinate ductis, an non sit axis, hoc est non ad rectos ipsis ordinate ductis, non refert: nam propositiones conicorum adductae ad omnem diametrum faciunt.