Si in quolibet triangulo linea basi aequidistans secet reliqua latera per aequalia, centrum gravitatis trianguli erit in trapetio ad basim relicto.

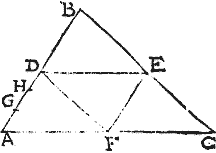
Sit triangulum ABC, in quo linea DE basi AC aequidistans secet AB, BC latera singula per aequalia in punctis D, E: aio quod centrum gravitatis trianguli ABC est in trapetio ADEC: secetur enim AC basis per aequalia in puncto F, et coniungantur DF, FE: quae per secundam sexti Euclidis, aequidistantes erunt ipsis AB, BC lateribus; unde triangulum ABC secatur in quatuor triangula sibi similia, et inter se aequalia, et aequilatera. Itaque per praecedentem, triangulorum ADF, FEC inter se aequilaterorum, et super unam lineam AFC, similiter positorum commune centrum est in linea aequidistante ipsi AFC, et secante caetera triangulorum latera: secabit igitur talis aequidistans ipsam AD secet in puncto G; per 3. autem huius, centrum gravitatis parallelogrammi BDFE est in diametro DE aequidistante iam ipsi AFC: cum igitur per centra partium eant duae aequidistantes, hoc est, quae per punctum G, et ipsa DE: quae scilicet per punctum G, per centrum commune triangulorum ADF, FEC tanquam unius partis, et ipsa DE per centrum parallelogrammi BF tanquam alterius partis: iam per 5. huius, aequidistans tertia, quae per centrum totius trianguli ABC media erit praedictarum: ibit igitur per medium punctum inter puncta D, G quod sit H: sed talis aequidistans ducta per punctum H fertur intra quadrilaterum ADEC: ergo centrum trianguli totius ABC, erit intra quadrilaterum ADEC: quod fuit demonstrandum.