Si duo triangula invicem aequilatera super eamdem lineam similiter posita sint; eorum centra, et commune centrum erunt in una recta aequidistante illi, super quam triangula sunt posita, secante et reliqua latera.

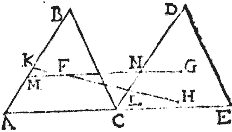
Sint duo triangula ABC, CDE invicem aequilatera, quorum bases ACE sint aequales, et in eadem recta. Item latus AB lateri CD, et reliquum reliquo aequale; et quorum centra gravitatum sint F, G: aio quod F, G centra sunt in linea aequidistante ipsi ACE: coniugatur enim FG, quae si non aequidistat ipsi ACE, aequidistet FH, et producta coincidat lateribus AB, CD apud K, L; eritque AKLC parallelogrammum: et perinde AK, CL aequales: quare BK, DL aequales; igitur cum linea KF per centrum eat trianguli ABC, aequidistans basi AC, et in triangulo simili CDE linea LH correlativo lateri CE aequidistans ad eandem rationem secet latus CD, ad quam latus AB secatur: iam ideo per 8. huius, LH ibit per centrum trianguli CDE: quod est impossibile: nam centrum per hypothesim est G punctum extra lineam LH: omnino igitur linea FG aequidistabit ipsi ACE sicut proponitur. Vel sic, per centrum F ducatur ipsi ACE aequidistans, lateribusque AB, CD apud M, N puncta coincidens MFN linea: eruntque in parallelogrammo AMNC latera AM, CN aequalia: et ideo BM, DN aequales: itaque linea MFN aequidistans basibus ACE ad eandem rationem secat latera AB, CD in punctis M, N, quae sunt latera correlativa similium triangulorum.

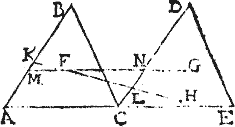
Itaque per centrum F trianguli ABC: igitur per 8. huius, linea MFN producta per centrum G trianguli CDE ibit: et perinde centra F, G sunt in linea MFNG aequidistante ipsi ACE, et per 6. praecedentis centrum commune triangulorum ABC, CDE in linea FG, sicut proponitur demonstrandum.