[A:8r]

<De centro solidi parabolae demonstratio acutissima¹ >

1 Centrum solidi conoidis parabolici trientem axis ad basim abscindit.

Hoc demonstraturi hasce conclusiones² tanquam lemmata praemittimus.

1.^a

2 Centrum uniformis³ figurae in puncto axis medio constituitur. Sive enim figura talis plana sit, ut parallelogrammum, sive solida, ut columna, sive cylindrus, hoc demonstratum in libello aequalium momentorum.

2.^a

3 Centrum trianguli rectilinei trientem axis ad basim relinquit. Appello hic axim eam rectam, quae a vertice trianguli deducta basim per aequalia secat. Hoc et in libello praedicto demonstratum est.

3.^a

4 Centrum totius interiacet centris partium in eadem recta constitutum.

4.^a

5 Centrorum partialium distantiae a centro totius reciprocae sunt partibus. Nec minus hae duae conclusiones ibidem demonstratae sunt in elementis.

5.^a

6 Centrum nunquam cadit extra rei gravis ambitum. Hoc enim tanquam concessibile, immo necessarium suppositum, haud quisque sanae mentis negaverit^[1].

7 Quibus quidem quinque propositionibus praemissis, demonstrabo id, quod in principio proposui, aliquibus praeambulis.

6.^a

8 Si rectilineum trigonum, axe per aequalia segmenta divisa, parallelogramma per singula divisionum puncta, et scalarem figuram⁴ facientia circumscribat: partiales autem parallelogrammorum axes in sextantes singuli secentur; tunc centrum parallelogrammorum erit sextante inferius centro trigoni, et centrum relictarum portionum sextante totalis axis superius centro parallelogrammorum, sive scalaris figurae.

9 Haec propositio tota sequitur ex praemissis consyderato centro totalis trigoni, centrisque partium, hoc est scalaris figurae atque relictarum portionum, quorum intervalla oportet esse [A:8v] reciproca partibus.

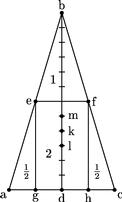
10 Dividatur enim in trigono abc axis bd primum bifariam: et latera ab bc singula bifariam et describatur parallelogrammum efgh sectoque axi bd in 12 partes aequales; erit centrum trigoni punctum k relinquens kd trientem totalis axis, per 2.^am praemissarum. Centrum autem parallelogrammi fg punctum l medium axis partialis per primam. Centrum denique relictarum portionum, hoc est triangulorum ebf, aeg, efh (per 2.^am, 3.^am et 4.^am) fiet in puncto m, ita ut tam kl quam km sit sextans axis partialis, quandoquidem⁵ parallelogrammum aequetur triangulis atque lm sextans totalis.

11 Sic constat ratio distantiae in centris et gravitatum, ut paucis agam tecum, cui haec omnia sunt trita et notissima.

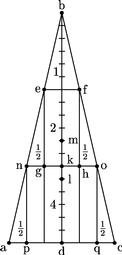
12 Rursum dividatur axis bd et latera ab bc singula in tria segmenta et inscribantur parallelogramma fg quidem quod prius et nopq, divisis quoque axibus in sextantes, erit centrum trianguli abc punctum k relinquens kd trientem axis bd ut prius; centrum autem parallelogrammorum fg, nq punctum l per sextantem inferius puncto k per primam et 4.^am6 praemissarum. 13 Centrum denique relictarum portionum (quae sunt triangula ebf neg ofh anp coq) punctum m, ita ut mk sit dupla ipsius kl per doctrinam 2.^ae, 3.^ae et 4.^ae [A:9r] praemissarum, quandoquidem parallelogramma dupla⁷ sunt relictarum portionum. Atque ita sicut kl sextans est axis partialis, ita lm sextans totalis, ut prius, atque sicut propositio concludit.

14 Item dividatur axis bd et latera ab bc singula quadrifariam et inscribantur parallelogramma fg nq quae prius et rstv⁸, divisis axibus singulis in sextantes. Eritque trigoni abc centrum in puncto k relinquens kd trientem axis totalis. Centrum autem dictorum parallelogrammorum fg nq st, hoc est scalaris figurae, punctum l per sextantem axis partialis infra punctum k. 15 Centrum demum relictarum portionum (quae sunt triangula ebf neg ofh rnp soq art csv) punctum m. Ita ut mk sit tripla ipsius kl per 2.^am, 3.^am et 4.^am praemissarum, quandoquidem scalaris figura ex tribus praedictis parallelogrammis constans triplum facit relictarum portionum. 16 Atque ita sicut kl sextans est axis partialis, ita lm sextans axis totalis, ut prius et sicut demonstrandum proponitur.

17 Adhuc dividatur axis bd et latera ab bc singula in quinque segmenta aequalia et inscribantur parallelogramma fg nq st quae prius; et xyzi divisis axibus in sextantes. Factoque calculo gravitatum et distantiarum, statuetur centrum trianguli abc punctum k ut kd sit triens axis totalis. 18 Centrum autem scalaris figurae compositae ex dictis parallelogrammis, punctum l, per sextantem axis partialis inferius puncto k.

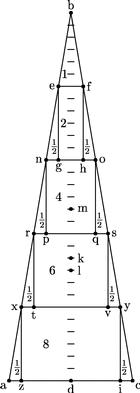
19 Centrum vero [A:9v] relictarum portionum (quae sunt triangula ebf neg ofh rnp soq xrt ysv axz cyi) punctum m. 20 Ita ut mk sit quadrupla ipsius kl per 2.^am, 3.^am et 4.^am praemissarum, quoniam scilicet scalaris figura ex quatuor dictis parallelogrammis constans, quadrupla est relictarum portionum. 21 Atque ita et hic demum, sicut kl sextans est axis partialis, ita lm sextans axis totalis, ut prius et ut demonstrandum fuerat.

22 Quod si axis bd et latera ab bc singula secentur in sex⁹ segmenta, id idem sequeretur. Et deinceps, si in septem¹⁰, aut 8¹¹, vel plura segmenta divisionem patiantur. 23 Verum sicut in prima descriptione kl spacium fuerat pars duodecima totalis axis bd, in secunda autem descriptione pars decima octava eiusdem, in tertia vero pars vicesima quarta et in postrema pars tricesima; ita, si axis bd secaretur in sex partes, kl esset 1/36 axis bd; si in 7 partes, esset 1/42; si in 8, esset 1/48 eiusdem axis. Atque ita deinceps in infinitum.

24 Hinc sequitur hoc Corollarium¹²:

25 <1.^um> Axis rectilinei trianguli potest dividi in tot partes aequas, ut distantia centrorum trianguli ipsius, et figurae scalaris triangulo inscriptae sit minor quocumque dato spacio.

26 <2.^um> Constat praeterea quod proportio triangulorum partialium a vertice b receptorum scilicet ebf nbo rbs xby abc procedit successive secundum proportione quadratorum numerorum ab unitate [A:10r] per ordinem sumptorum scilicet 1, 4, 9, 16, 25. Et deinceps sequentium, si plures essent divisiones.

27 <3.^um> Quare trianguli primi et succendentium trapeziorum hoc est trianguli ebf, trapeziorum fn ns sx xc proportio erit et quae numerorum imparium ab unitate continuatorum hoc est 1, 3, 5, 7, 9 et deinceps.

28 <4.^um> Item quadrilatera fg nq st xJ erunt in proportione numerorum ab unitate per naturale unitatis crementum ordinatorum scilicet 1, 2, 3, 4, et deinceps in infinitum.

29 <5.^um> Demum relictae portiones, hoc est triangulum primum et deinde bina queque parallelogrammorum collateralia triangula¹³ procedunt per aequalitatem.

30 Verum bina triangula primo parallelogrammo collateralia sunt eius dimidium. Bina secundi quadrans. Bina tertii sextans. Bina quarti pars octava. Itaque deinceps.

31 Quibus consyderatis procedemus ad demonstrandum propositum de parabolici solidi centro hactenus a nullo demonstratum.

7.^a

32 Solidum per paraboles periferiam super axe semel circumductam descriptum ad conum communis basis atque fastigii sesquialterum esse probatur.

33 Haec propositio in secundo Conoidum libello ab Archimede nostro demonstratur.

8.^a

34 Si parabolicum solidum per parallela plana, quibus axis rectus insistat, abscindatur: solidi segmenta ad verticem a planis recepta sunt sicut axium quadrata.

35 Haec quoque propositio in praedicto libello demonstratur, et ex praecedenti sequitur facillime, quandoquidem talia segmenta sunt conis eandem basim et eundem axem habentibus proportionalia.

9.^a

36 Si parabolici solidi axis in quotlibet partes aequales dividatur, et per puncta divisionum parallela plana in rectum axi ducantur; facta solidi segmenta, a planis ad verticem recepta, erunt per ordines in proportione quadratorum numerorum ab unitate seriatim dispositorum.

37 Haec propositio aptissime constat ex praecedenti.

[A:10v]

10.^a

38 Iisdem suppositis, si inter dividentia plana intelligantur Cylindri, quorum axes sint ipsius axis segmenta, proportio cylindrorum erit sicut proportio numerorum ab unitate per ordinem naturalis continuatorum.

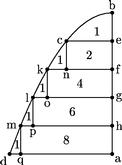
39 Esto axis paraboles ab, periferia bcd, basis ad; secetur ab in quotvis segmenta aequalia in punctis e f g h a quibus ad rectos ad periferiam ducuntur ec, fk, gl, hm et a punctis cklm ad ductas in rectum lineae cn, ko, lp, mq. 40 Sic enim circumducta semel super axe ab periferia bcd una cum rectis, periferia solidum parabolicum et rectae cylindros super axes ef, fg, gh, ha describent. 41 Ostendendum est igitur, quod cylindri cf kg, lh, ma et deinceps in infinitum sunt in proportione numerorum ab unitate et per unitatem crescentium. 42 Nam, sicut in Conicis ostensum est, sicut est  kf   ce sic fb   be. Igitur et sicut fb  be sic basis cylindri kg  basim cylindri cf; et ideo sicut cylindrus kg  cylindrum cf quandoquidem eiusdem celsitudinis¹⁴. Dupla autem est fb ipsius be. Ergo et cylindrus kg duplus cylindri cf, hoc est sicut 2  1. 43 Similiter omnino demonstrabitur cylindrus lh triplus esse cylindri cf, quia sicut gb  be. Et cylindrus ma quadruplus cylindri cf quoniam scilicet sicut hb  be. Et similiter sequens primi quincuplus atque ita in infinitum proportio a succedentibus per unitatem numeris continuatus demonstrabitur. Quod est propositum.

44 Ex his duabus propositionibus sequuntur totidem corollaria :

45 <1.^um> Parallelis planis per dicta divisionum aequalium puncta, praedicto modo solidum parabolicum dividentibus, solidi seg[A:11r]menta planis intercepta sunt in proportione imparium numerorum ab unitate per ordinem dispositorum.

46 Nam cum per antepraemissam, solida a planis ad verticem recepta sint in proportione quadratorum ab unitate per ordinem continuatorum. Et differentiae quadratorum sint impares ab unitate ordinati. Iam et ipsorum solidorum differentiae (quippe quae planis intercipiunt) erunt in eadem imparium proportione dispositae¹⁵.

47 <2.^um> Item ex praemissa sequitur, ut relictae portiones post subtractionem cylindrorum a dictis segmentis inter plana interiectis procedant per aequalitatem.

48 Verum prima portio erit dimidium cylindri. Secunda quadrans. Tertia sextans. Quarta vero portio fiet octava pars. Sicut procedebant portiones in triangulo. 49 Nam si ponatur primum segmentum solidi parabolici 1, sequens erit 3, tertium 5, quartum 7, quintum 9, et deinceps per numeros impares, per praemissum corollarium¹⁶ . Sed conus primi segmenti, per 7.^am praemissarum, erit tunc 2/3. Ergo cylindrus primus, (qui triplus est coni) fiet 2. Quare, per praecedentem, cylindrus sequens erit 4, tertius 6, quartus 8, et deinceps: qui cylindri singuli si subtrahantur a segmentis dictis inter plana clausis, hoc est 2 a 3, item 4 a 5, itemque 6 a 7, demum 8 a 9, semper relinquitur unitas. Quae primi cylindri est dimidium. Secundi quarta pars. Tertii sexta. Quarti octava et sicut corollarium infert.

50 Ex quibus manifestum est, quod diviso tam axe trianguli quam axe parabolici solidi in totidem cuiuslibet numeri aequales partes, factaque in triangulo scalari plana figura ex parallelogrammis, in solido autem scalari solida figura ex cylindris totidem constructa, tunc in triangulo [A:11v] partialia trigona a vertice recepta erunt partialibus solidis in solido item a vertice receptis. 51 Et in triangulo trigonum supremum, et trapezia succedentia erunt solido supremo et segmentis succedentibus proportionalia. Illa videlicet in proportione quadratorum, haec vero imparium numerorum ab unitate ordinatorum. 52 Item in triangulo relictae portiones ad collateralia parallelogramma: et in solido relictae portiones ad contiguos cylindros eandem proportionem servabunt, et invicem aequales existunt.

53 Quae omnia (quoniam collatio fit a planis ad solida) non modicam speculativis ingeniis admirationem ingerunt.

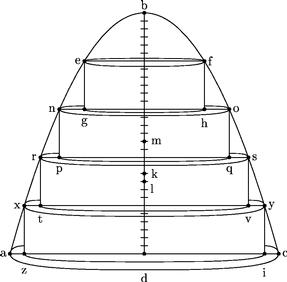
54 Sed eccam hic expositam parabolici solidi, ut dictum est, divisi, cum scalari figura ex cylindris divisionum structa et inscripta, descriptionem. Quare properemur ad id, quod de centro demonstrandum proposueramus. Sed praemittemus adhuc nonnulla demonstrationi necessaria praeambula.

11.^a

[A:12r] 55 Possibile est toties axem parabolici solidi modo¹⁷ iam memorato dispescere, ut scalaris figura ex cylindris divisionum composita, ad aggregatum relictarum portionum maiorem habeat proportionem, quacumque data proportione.

56 Nam per praecedentis ultimum corollarium, dicta scalaris solida figura ad relictas portiones eandem proportionem servat, quam scalaris figura plana in triangulo ad suas relictas portiones (facta utrobique eiusdem numeri divisione). 57 Sed, per 6.^am praemissarum, in prima descriptione, parallelogrammum aequum est portionibus relictis. In 2.^a duo parallelogramma duplum sunt relictarum portionum. In 3.^a scalaris figura ex parallelogrammis tripla est relictarum portionum. In 4.^a quadrupla. In 5.^a quincupla. 58 Et ita deinceps, centupla, millecupla, aut millies millecupla¹⁸ et in infinitum crescens¹⁹, et perinde²⁰ sic cylindrica scala²¹ ad suas portiones ad maiorem quacumque data proportione redigi potest. Quod est propositum.

12.^a

59 Secto axe parabolici solidi in partes quotvis aequales, quae sunt axes totidem cylindrorum scalarem figuram solido inscriptam componentium: axibus in sextantes divisis, punctoque assumpto, quod ex axe totius solidi trientem versus basim relinquat; tunc centrum scalaris figurae erit per sextantem axis partialis puncto assumpto inferius. Et centrum²² relictarum portionum sextante totalis axis superius eodem puncto.

60 Nam cum in triangulo, ut in 6.^a traditum est, diviso, parallelogramma scalarem figuram facientia, per 4.^um eiusdem corollarium procedant secundum proportionem numerorum ab unitate secundum naturalem ordinem crescentium, et diviso parabolico solido, sicut 9.^a et 10.^a docent, cylindri scalarem in eo figuram componentes, per demonstrationem decimae, servent dictam numerorum proportionem. 61 Atque cum ipsi cylindri sint sicut parallelogramma, uniformes et centrum in medio axis sortiantur: iam demonstrabitur haec propositio per eadem, omnino, per quae ostensum est in 6.^a punctum l, quod [A:12v] est centrum figurae scalaris, esse semper inferius puncto k, quod trientem kd abscindit de toto axe ad basim, per dicti sextantis spacium: quod hic de scala cylindrica proponitur demonstrandum. Et²³ similiter de centro relictarum portionum: quod proponitur.

62 Unde sequitur corollarium.

Possibile est axem parabolici solidi toties modo praedicto secari, ut distantia inter centrum scalae cylindricae et punctum, quod de axe trientem versus basim relinquit, sit minor quocumque dato spacio.

63 Non aliter hoc procedit, quam primum corollarium sextae.

13.^a

64 Quibus iam praemissis, ita quod in principio proposuimus ostendemus.

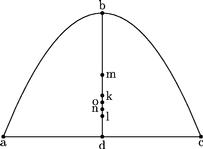
65 Esto parabolicum solidum, quod a parabola abc circum axim bd circumductam describitur, cuius basis adc. Sitque in axe punctum k de axe ipso kd trientem versus basim relinquens. 66 Ostendendum est, quod k punctum est huiusmodi solidi centrum. Sic. Si centrum solidi talis non sit k punctum; erit centrum in alio puncto, aut infra, aut supra punctum k. 67 Sit primum infra in puncto n. 68 Et tunc²⁴ possibile erit , per praecedentis corollarium, axem solidi toties secari, ut centrum scalae cylindricae per minus spacium accedat puncto k, quam punctum n, hoc est ut minor sit distantia dicti centri²⁵ a puncto k quam spacium nk. 69 Sit ergo centrum²⁶ scalae in o puncto inter k n puncta. Et²⁷ centrum relictarum portionum in puncto m. Eritque centrum totius solidi n extra centra partium, hoc est non interiacebit ipsis punctis o m, quae sunt centra scalae et portionum, quae sunt partes solidum integrantes. 70 Quod est absurdum, per tertiam [A:13r] praemissarum propositionum. Non igitur cadet centrum solidi infra punctum k. //

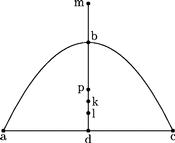
71 Cadat, si possibile est, supra punctum k utpote in punctum p. 72 Atque punctum l ponatur centrum scalae cylindricae. Deinde dividatur axis toties, ut dictum est, constructis cylindris; ut cylindrica figura ad relictas portiones maiorem habeat proportionem, quam linea bp  linea pl utpote eam proportionem, quam habet linea mp  lineam pl. Hoc²⁸ enim possibile est per 11.am. 73 Cumque p sit centrum totius solidi: l vero centrum unius partium, scilicet scalae cylindricae: iam per 4.^am praemissarum m erit centrum reliquae partis, scilicet relictarum portionum. 74 Quod per quintam praemissarum est impossibile. Quandoquidem centrum extra rei gravis ambitum cadere absurdum est. 75 Non igitur cadet solidi centrum²⁹ supra punctum k. Sed neque infra illud cadere posse ostensum est. Omnino igitur ipsum k punctum erit solidi centrum. 76 Quod demonstrandum proponebatur.

* Corollaria

77 <1.^um> Et quoniam per 12.^am centrum scalae est per sextantem unius axium particularium inferius puncto k quod centrum esse totius nunc ostensum est. Sequitur ut centrum relictarum portionum per sextantem totalis axis sit superius centro scalae: sicut in triangulo fiebat. Propter proportionalitatem partium et totius in triangulo et solido sumptarum.

78 <2.^um> Sequitur etiam, tam in triangulo, quam in solido parabolico, ut sextans totalis axis ad sextantem unius axium partialium in ea sit proportione, in qua totale triangulum ad relictas portiones sive totale solidum ad relictas portiones. Quod per quartam propositionem et coniunctam proportionalitatem constat.

79 Et haec hactenus.

5.^o30 maii 1565