49

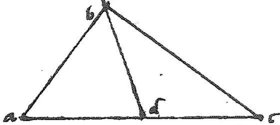
150 Pyramis, octahedrum, cubi duo, angulariter ad unam rectam compositi quatuor rectorum angulorum spatium perfecte consummant. Hoc in 17^o satis liquet ostendetur et hic aliter, ne semel incepta series interrumpatur. Sit itaque triangulum abc rectum, qui ad b angulum habens, sitque ipsumac latus potentialiter ad¹³³ ab triplum: quo fiet ut ac ad ipsum bc potentialiter sit sesquialterum. 151 Et secta bifariam ac in signo d erunt tria brachia¹³⁴ ad, db, dc invicem aequalia: circulus enim super centrum d ad spatium da descriptus transit per signum b alias mentiretur 29^a tertii. Quoniam itaque ac¹³⁵ ad ipsum ab potentia triplum est ad ipsam vero dc vel ad¹³⁶ quadruplum, erit ab ad ipsam ad vel¹³⁷ db potentia sesquitertium¹³⁸. Quare per 29^um cap. adb angulus erit pyramidis¹³⁹. 152 Item quoniam ac¹⁴⁰ ad ipsum bc¹⁴¹ sesquialterum est, ad ipsam vero dc quadruplum: erit bc ad ipsam cd vel db potentialiter duplum superpartiens duas tertias, hoc est sicut 8 ad 3. Quare per 23^um cap. bdc angulus est octahedri. Vides igitur angulum adb pyramidis et angulum bdc octahedri simul iunctos perficere duos rectos. Sed [A:15r]duo cubi perficiunt duos rectos, quandoquidem, per 22^am cubi angulus rectus est. Ergo pyramis et octahedrum cum duobus cubis quatuor rectos consummabunt angulos.