[A:12r]

42

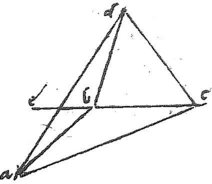
123 Tres pyramides cum uno dodecahedro non totum complebunt locum. Ex 37^o cap. sumo angulum abd compositum ex duobus angulis pyramidis, cui aequalem facio angulum abc cui annecto angulum cbd pyramidis: factisque brachiis ab, bc, bd invicem aequalibus, connectantur ac, cd et producatur cb ad signum e eritque angulus abd obtusus complementum trium angulorum pyramidis ad quatuor rectos, nam tres pyramidis anguli excedunt duos rectos. 124 Angulus itaque eba per 32^am p ⁱ⁹⁷ aequalis est duobus angulis bac, bca et per eandem angulus ebd aequalis erit angulis bdc et bcd cumque anguli bac, bca per 5^am primi sint invicem aequales: et anguli bdc, bcd invicem aequales, erit angulus abd duplus ad angulum acd. Duplicabo igitur angulum acd et sic habebo angulum abd cui conferam angulum icosahedri, ut appareat defectus localis complementi. 125 Ponam itaque ipsi abc⁹⁸ simile et aequum triangulum fgh ita ut angulus fgh ipsi angulo abc⁹⁹ sit aequalis: item faciam ipsi cbd simile et aequum triangulum hkf ita ut angulus hkf aequalis sit angulo cbd, et connexa gk, quae secet fh in puncto l,¹⁰⁰ faciam ipsi kfg simile et aequum triangulum kfm ita unde anguli kfg, kfm sint invicem aequales et anguli fkg, fkm invicem aequales: et connectatur gm eruntque tres anguli ad signum k invicem aequales: quare anguli hkf, gkm invicem aequales, et ideo triangula hkf, gkm similia. 126 Sed per 37^um cap., posito hf quadrato 96, fiet quadratum fg 27, et per 21^um cap. quadratum fk 72: unde¹⁰¹ quadratum gl fiet 3, quadratum vero lk 48, quae si iungatur per regulam iungendi quadrata, fiet quadratum gk 75. Sed propter¹⁰² triangulorum similitudinem, sicut kf ad fh sic kg ad gm. Multiplico igitur 96, quod est quadratum fh, in 75, quod est quadratum kg et exeunt 7200, quod divido in 72, quod est quadratum kf, et prosiliunt ex divisione 100, quod est quadratum gm. Sed quadratum fg fuit 27, eritque angulus gfm duplus ad angulum gfk, et ideo duplus ad angulum acd, et ideo aequalis angulo abd. 127 Quare ad potentialiter ad ab sicut 100 ad 27. Sed latus subtendens angulum dodecahedri ad suum brachium potentialiter minor est quam 100 ad 34 per 24^um cap.¹⁰³ ergo [A:12v]a fortiori minor quam da ad ab. Quare per 26^um cap. angulus abd maior angulo dodecahedri. Sed angulus abd est id, quod superest post connexionem trium angulorum pyramidis. Igitur tres pyramides cum uno dodecahedro angulariter¹⁰⁴ coniunctae vacuum in medio relinquunt.