16^a Si per bifariam sectionem transversi lateris contrapositarum sectionum ducatur quaedam linea ordinate applicata; diameter erit coniugata praeexistenti diametro

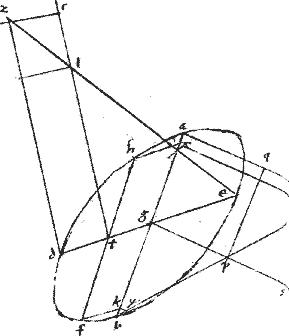
Contrapositarum diameter ab bifariam secetur in puncto g et ordinata ducatur dg²³⁹.

// Aio quod dg²⁴⁰ est coniugata diameter ipsi ab diametro.

// Sint enim,

ad quas possunt hyperbolarum contrapositarum ordinatae²⁴¹ ae bz. Et connectantur az be. // Et per contingens in altera sectionum punctum h²⁴² penes ab ducatur ht. // Et ordinate ducantur hc tl. // Et gd²⁴³ producta secet ipsam ht in puncto x. // Item cm ln penes ipsas ae bz.

// Et quoniam, per 34^am primi Euclidis hc tl aequales²⁴⁴: ideo et hc tl aequalia. // Sed per 12^am huius hc aequale^{245 lo} hcm²⁴⁶. Itemque²⁴⁷ tl aequum bln. // Ergo acm bln aequalia²⁴⁸.

// Et quoniam, per 14^am huius, ae bz aequales²⁴⁹: ideo ae ab sicut²⁵⁰ bz ba. // Et propter aequidistantiam linearum mc cb sicut²⁵¹ nl la.

// Sed per primam 6ⁱ Euclidis sicut mc cb sic mca bca. // Itemque sicut²⁵² nl la sic nlb alb.

// Igitur sicut mca bca sic nlb alb. // Et permutatim sicut mca nlb sic bca alb.

// Verum fuit mca aequale nlb. // Ergo et bca aequale^{253 lo} alb.

[A:11r] // Quare per 14^am 6ⁱ Euclidis sicut bc bl sic al ac. // Et coniunctim, sicut cl lb sic lc ca²⁵⁴.

// Et ideo per 9^am 5ⁱ Euclidis ca aequalis²⁵⁵ lb.

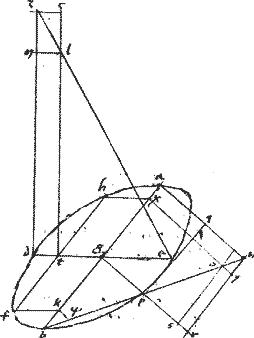
// Sed ag aequalis²⁵⁶ gb. Igitur tota gc aequalis toti gl.

// Quare et hx aequalis²⁵⁷ xt hoc est ht ipsi ab aequedistans bifariam secatur per gd²⁵⁸ ordinatam.

// Similiter ostendam quod gd²⁵⁹ bifariam secat omnem parallelum ipsius ab inter sectionum periferias²⁶⁰ actam. Quare per diffinitionem gd²⁶¹ est diametros²⁶² ipsi ab diametro coniugata: quod erat demonstrandum.

Iam igitur, sicut ab prima diametros,ut in 7^a huius ostensum est , secabat ordinatas ipsius dg²⁶³ parallelos intra utriusvis sectionis periferiam ductas bifariam: ita nunc, ut praesens ostendit, ipsa dg²⁶⁴ secat et bifariam ipsa ht omnemque aliam²⁶⁵ ipsius ab parallelum. // Exterius²⁶⁶ ad hyperbolarum periferias applicatam. Ideoque secunda diametros iure vocatur. // Sunt ergo ab gd²⁶⁷ coniugatae diametri, cum earum utraque alterius parallelis²⁶⁸ in periferiis sectionum terminatas bifariam singulas dispescat, sitque ob id, utraque respectu alterius diametros.