15a. Si a bifaria sectione diametri208 ellipsis ordinata recta ducatur utrinque ad periferiam ellipsis: sitque ut ordinata ad diametrum, sic diameter ad tertiam quamdam; tunc, quae ducitur a periferia ad ordinatam, aequidistans diametro, poterit, quod superficies adiacens209 ad tertiam, latitudinem habens sub ipsa receptam ex ordinata ad periferiam, deficiens specie simili contento sub ordinata et tertia: et producta usque ad alteram partem periferiae bifariam secabitur ab ordinata.
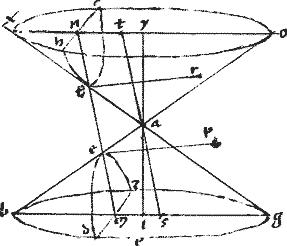
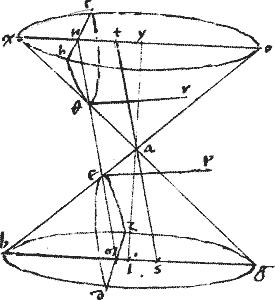
[S:17] Sit ellipsis210, cuius diameter ab bifariam secetur in puncto g et ordinata ducatur dge. // Sitque sicut de ![]() ab sic ab
ab sic ab ![]() dz ad rectos ipsi de. // Et [[qui]] contingens punctum211 h in periferia agatur ht penes ab diametro212. // Et connectatur ez. // Ducaturque tl penes dz compleaturque parallelogrammum lczm
dz ad rectos ipsi de. // Et [[qui]] contingens punctum211 h in periferia agatur ht penes ab diametro212. // Et connectatur ez. // Ducaturque tl penes dz compleaturque parallelogrammum lczm ![]() lum.
lum.
// Dico iam primum213 quod ht potest ![]() dl adiacens ad dz latitudinem habens dt et deficiens specie lz simili
dl adiacens ad dz latitudinem habens dt et deficiens specie lz simili ![]() lo edz.
lo edz.
// Sit enim per 13am huius: ipsa an ad quam possunt ordinatae ad ab diametrum. // Et agatur hx penes de. // Item xo gp penes an. // Et productae compleant214 ![]()
![]() qo ops215 sry, oyn.
qo ops215 sry, oyn.
// Itaque per 13am praemissam dg potest ![]() ap. // Et hx potest
ap. // Et hx potest ![]() ao. // Et quoniam ag gb aequales216, ideo
ao. // Et quoniam ag gb aequales216, ideo ![]()
![]() ap qr aequalia217: et similiter
ap qr aequalia217: et similiter ![]()
![]() xq qy aequalia invicem.
xq qy aequalia invicem.
// Item quoniam, per 43am primi Euclidis supplementa oq or sunt aequalia: posito iam communi ![]() no218 erunt
no218 erunt ![]()
![]() qy ns invicem aequalia: et ideo
qy ns invicem aequalia: et ideo ![]()
![]() la xq [[ ns]] aequalia. // Positoque communi
la xq [[ ns]] aequalia. // Positoque communi ![]() qs erit
qs erit ![]() np vel
np vel ![]() ap aequale gnomoni219 aop. // Igitur
ap aequale gnomoni219 aop. // Igitur ![]() dg (quod est ipsum
dg (quod est ipsum ![]() ap) maius est, quam
ap) maius est, quam ![]() hx (quod est ipsum
hx (quod est ipsum ![]() ao ) in
ao ) in ![]() op. // Sed, per 5am 2i Euclidis
op. // Sed, per 5am 2i Euclidis ![]() etd una cum
etd una cum ![]() tg sive hx aequale est
tg sive hx aequale est ![]() dg.
dg.
// Igitur ![]() etd aequale est
etd aequale est ![]() lo op. // Et quoniam de ab dz sunt in proportione continua. Ideo per 17am 6i220 Euclidis sicut de
lo op. // Et quoniam de ab dz sunt in proportione continua. Ideo per 17am 6i220 Euclidis sicut de ![]() dz sic
dz sic ![]() de
de ![]()
![]() ab et sic
ab et sic ![]() dg
dg ![]()
![]() gb quandoquidem dimidia integris sunt proportionalia. [A:10r] // Sed per primam sexti Euclidis
gb quandoquidem dimidia integris sunt proportionalia. [A:10r] // Sed per primam sexti Euclidis ![]() etd
etd ![]()
![]() dtl sicut221 et
dtl sicut221 et ![]() tl et ideo sicut de
tl et ideo sicut de ![]() dz.
dz.
Ergo, sicut ![]() dg
dg ![]()
![]() gb sic
gb sic ![]() etd
etd ![]()
![]() dtl. // Cumque
dtl. // Cumque ![]() pgb aequale sit
pgb aequale sit ![]() ap et ideo ipsi
ap et ideo ipsi ![]() to dg sitque per primam 6i
to dg sitque per primam 6i ![]() pgb
pgb ![]()
![]() gb sicut pg
gb sicut pg ![]() gb.
gb.
// Erit et similiter ![]() dg
dg ![]()
![]() gb sicut pg
gb sicut pg ![]() gb.
gb.
// Et ideo sicut pg ![]() gb sic
gb sic ![]() etd
etd ![]()
![]() dtl.
dtl.
// Sed sicut pg ![]() gb sic ps
gb sic ps ![]() so et ideo per primam 6i sicut
so et ideo per primam 6i sicut ![]() pso
pso ![]()
![]() os.
os.
// Igitur sicut ![]() pso
pso ![]()
![]() os sic
os sic ![]() etd
etd ![]()
![]() dtl.
dtl.
// Sed dudum aequale fuit ![]() pso
pso ![]()
![]() etd.
etd.
// Ergo per 14am 5i ![]() os hoc est
os hoc est ![]() ipsius ht aequale erit
ipsius ht aequale erit ![]() dtl. // Quod erat ex demonstrandis primum. // Sed222 ducatur ht ad periferiam usque ellipseos ad punctum f.
dtl. // Quod erat ex demonstrandis primum. // Sed222 ducatur ht ad periferiam usque ellipseos ad punctum f.
// Aio deinde quod producta hf bifariam secatur ad ipsa de apud punctum t.
// Agatur enim ipsi hx aequidistans fk nec non k![]() penes ipsam an usque ad bn.
penes ipsam an usque ad bn.
// Eritque per 13am praecedentem ![]() fk aequale
fk aequale ![]() lo ak
lo ak![]() et quadratum hx aequale
et quadratum hx aequale ![]() lo ao cumque sint
lo ao cumque sint ![]()
![]() fk hx aequalia (quoniam lineae ipsae aequales) erunt et
fk hx aequalia (quoniam lineae ipsae aequales) erunt et ![]()
![]() ak
ak![]() ao aequalia.
ao aequalia.
// Quamobrem per 15am 6i223 xo ad k![]() sicut224 ak
sicut224 ak ![]() ax. // Sed propter
ax. // Sed propter ![]()
![]() bxo bk
bxo bk![]() similitudinem bx
similitudinem bx ![]() bk sicut225 xo
bk sicut225 xo ![]() k
k![]() .
.
// Igitur ak ![]() ax sicut226 bx
ax sicut226 bx ![]() bk.
bk.
// Et disiunctim kx ![]() xa sicut227 xk
xa sicut227 xk ![]() kb.
kb.
// Quare per 9am 5i ax kb aequales228. // Sed ga gb aequales229. // Ergo gx gk aequales230. Et ideo th tf aequales: quod restabat231 demonstrandum.
Manifestum est232 ergo quod in ellipsi ab de sunt coniugatae diametri: namque per 7am ab secat ipsam de eiusque parallelas bifariam: itemque de. Sicut praesens ostendit, secat ipsam hf omnemque ipsius ab parallelum bifa[A:10v]riam. // Item sicut respectu ab primae233 diametri, seu234 transversi lateris, rectum latus, hoc est, ea, ad quam possunt ordinate ad diametrum fuit ipsa an linea. Ita, respectu235 de secundae diametri, seu transversi lateris rectum latus, sive ad quam possunt ordinatae ad ipsam diametrum, erit ipsa dz. [[// ]] Ac demum, sicut est secunda diametros inter primam suamque rectam media proportionalis: ita et prima diametros est inter secundam; suamque [S:18] rectam itidem media proportionalis. Unde utraque potest species alterius. Cum species sit ![]() sub transversa236 et recta237 diametris contentam238.
sub transversa236 et recta237 diametris contentam238.