[A:12r] ELEMENTORUM QUINTUS
1 Commensurabiles magnitudines sunt; quas una communis magnitudo metitur. Incommensurabiles vero, quas nulla communis mensura numerat. Unde1 omnes duo numeri sunt invicem commensurabiles quoniam mensurantur ab unitate.
2
Ratio est magnitudinum duarum eiusdem generis2 collatio.
Similes, eaedem3 vel aequales rationes dicuntur4, quae vel sunt eiusdem nominis, vel ad quamlibet, nominatam rationem collatae semper sunt ea vel5 simul maiores vel simul minores.
3
Proportio est rationum similitudo, identitas vel aequalitas.
Eandem rationem habentes magnitudines prima ad secundam et tertia ad quartam, proportionales dicuntur.
4
Si prima ad secundam magnitudinem rationem habeat, quam secunda ad7 tertiam et quam tertia ad quartam et deinceps similiter; continue proportionales magnitudines dicuntur. Et tunc prima ad tertiam duplicatam rationem habere dicetur eius, quam prima ad secundam. Sed prima ad quartam triplicatam eius, quam prima ad secundam. Et deinceps.
Communes animi conceptiones
5
Aequales magnitudines ad tertiam quamlibet collocatae eandem habent rationem. Contra si eandem habeant rationem ad tertiam, sunt aequales.
Quaelibet magnitudo ad duas aequales collata eandem habet rationem. Contra si eandem illae sunt aequales.
6
Binae magnitudines binis magnitudinibus singulae singulis aequales8 sunt proportionales.
Inaequalium magnitudinum maior ad tertiam maiorem habet rationem. Et si maiorem; maior erit.
7
Quaelibet magnitudo ad duas inaequales magnitudines collata maiorem rationem habet ad minorem. Et si maiorem, illa ex duabus minor erit. [A:12v] Rationes duae, quae tertiam adaequant rationem sunt invicem aequales.
8
Rationes aequales rationibus aequalibus continuatae componunt rationes aequales. Ab aequalibus ablatae, relinquunt aequales. Rationes9 aequalium rationum aeque multiplices sunt aequales. Et e converso.
9
Inaequales vero aequalibus continuatae10, componunt inaequales, et ablatae relinquunt inaequales. Aequales11 rationes ad tertiam collatae sunt vel illi simul aequales vel simul maiores vel simul minores.
Propositiones
pa
10
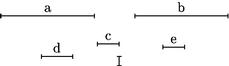
Magnitudines commensurabiles sunt proportionales numeris. Sunto duae magnitudines a, b commensurabiles et earum communis mensura c quae metiatur ipsam a secundum numerum d ipsam vero b12 secundum numerum e. Atque ita quoniam a habet13 tot partes quot unitates habet numerus d. Et b tot partes, quot unitates habet numerus e erit sicut a![]() c sic d
c sic d![]() unitatem.
11
Et sicut c
unitatem.
11
Et sicut c![]() b sic unitas
b sic unitas![]() e. Ergo per 7am conceptionem, erit a
e. Ergo per 7am conceptionem, erit a![]() b sicut d
b sicut d![]() e quod est propositum ***14 ratio.
e quod est propositum ***14 ratio.
2a
12 Magnitudinum commensurabilium ratio nominata est. Quoniam scilicet15, per praecedentem, est ratio notorum numerorum: et ab ipsis nominatur.
3a
13
Omnis magnitudinum ratio aut nominata est, aut nominatis interiacet16 rationibus. Nam si magnitudines sint commensurabiles, tunc, per praemissam, ratio nominata est. Ut ab![]() bc. Si autem incommensurabiles: tunc d metiatur ipsam ab.
14
Et eadem d metiatur ipsam be minorem quam bc et ipsam bf maiorem, atque ratio ab
bc. Si autem incommensurabiles: tunc d metiatur ipsam ab.
14
Et eadem d metiatur ipsam be minorem quam bc et ipsam bf maiorem, atque ratio ab![]() bc minor erit, quam ratio ab
bc minor erit, quam ratio ab![]() be nominata: et maior; quam ratio ab
be nominata: et maior; quam ratio ab![]() bf nominata (per 5am conceptionem)17 [A:13r] interiacens scilicet ipsis
bf nominata (per 5am conceptionem)17 [A:13r] interiacens scilicet ipsis
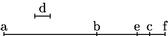
4a
15 Magnitudines proportionales numeris sunt commensurabiles.
Sit magnitudo a![]() magnitudinem b sicut numerus d
magnitudinem b sicut numerus d![]() numerum e. Dividatur a in tot partes, quot unitates sunt in numero d quarum partium una sit c. Eritque unitas
numerum e. Dividatur a in tot partes, quot unitates sunt in numero d quarum partium una sit c. Eritque unitas ![]() d sicut c
d sicut c![]() a.
16
Estque per hypothesim sicut d18
a.
16
Estque per hypothesim sicut d18![]() e sicut a
e sicut a![]() b. Ergo per 7am conceptionem unitas
b. Ergo per 7am conceptionem unitas![]() e sicut c
e sicut c![]() b. Sed unitas metitur numerum e. Ergo c magnitudo metitur magnitudinem b. Sed c metiebatur ipsam a. Ergo a, b commensurabiles.
b. Sed unitas metitur numerum e. Ergo c magnitudo metitur magnitudinem b. Sed c metiebatur ipsam a. Ergo a, b commensurabiles.

5a
17 Si ratio magnitudinum sit nominata; magnitudines sunt commensurabiles. Nominatur enim ratio a numeris, quibus magnitudines sunt proportionales per pam19 et ideo per praecedentem, ipsae magnitudines sunt commensurabiles.
6a
18 Magnitudines incommensurabiles non sunt sicut numerus ad numerum. Nam si sunt sicut numerus ad numerum, per20 antepraemissam, sunt commensurabiles quod est contra hypothesim astruitur ergo propositum.
7a
19 Magnitudines quae non sunt sicut numerus ad numerum sunt incommensurabiles. Nam si commensurabiles: tunc per pam horum, erunt sicut numerus ad numerum, quod est contra hypothesim astruitur ergo propositum.
8a
20 Si partes fuerint proportionales partibus in eiusdem nominis ratione. Et totum toti erit in eadem ratione. Quia quoties communes mensurae metiuntur21 singulas partes; toties aggregatum mensurarum metitur aggregata partium. Et perinde aggregata partium dividentur in numeros22 earum portionum, in quos dividuntur partes. Et ideo erunt in [A:13v] eiusdem nominis ratione.
9a
21
Si partes partibus sunt proportionales: erit sicut pars ad partem; sic totum ad totum. Sit sicut ab![]() de sic bc
de sic bc![]() ef. Dico quod erit, sic ac
ef. Dico quod erit, sic ac![]() df. Nam si rationes sint nominatae, constat propositum per praemissam. Secus autem23 tales proportiones, per 3am, interiacebunt nominatis rationibus.
22
Sit itaque ratio: ab
df. Nam si rationes sint nominatae, constat propositum per praemissam. Secus autem23 tales proportiones, per 3am, interiacebunt nominatis rationibus.
22
Sit itaque ratio: ab![]() de minor, quam ab
de minor, quam ab![]() eg nominata: eritque per diffinitionem similium rationum, ratio bc
eg nominata: eritque per diffinitionem similium rationum, ratio bc![]() ef minor quam ratio bc
ef minor quam ratio bc![]() eh nominata eiusdem nominis. Verum per praemissam, ratio totius ac
eh nominata eiusdem nominis. Verum per praemissam, ratio totius ac![]() totam gh est sicut ab
totam gh est sicut ab![]() eg vel bc
eg vel bc![]() eh in eiusdem nominis rationem.
23
Minor24 autem est ac
eh in eiusdem nominis rationem.
23
Minor24 autem est ac![]() df quam ac
df quam ac![]() gh. Ergo et minor est ac
gh. Ergo et minor est ac![]() df quam ab
df quam ab![]() eg et quam bc
eg et quam bc![]() eh. Et similiter ostendam, quod quacumque ratione nominata minor est ratio ab
eh. Et similiter ostendam, quod quacumque ratione nominata minor est ratio ab![]() de vel bc
de vel bc![]() ef hac ipsa minor erit ratio ac
ef hac ipsa minor erit ratio ac![]() df. Et quacumque maior; maior. Quare per conversionem diffinitionis similium rationum, erit sicut ab
df. Et quacumque maior; maior. Quare per conversionem diffinitionis similium rationum, erit sicut ab![]() de vel bc
de vel bc![]() ef sic ac
ef sic ac![]() df quod fuit demonstrandum.
df quod fuit demonstrandum.

10a
24
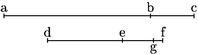
Si totum ad totum fuerit sicut ablatum ad ablatum erit residuum ad residuum sicut totum ad totum. Sit ac![]() df sicut ab
df sicut ab![]() de. Dico iam quod erit bc
de. Dico iam quod erit bc![]() ef sicut ac
ef sicut ac![]() df. Nam secus sit bc
df. Nam secus sit bc![]() eg25 sicut ac
eg25 sicut ac![]() df et ideo sicut ab
df et ideo sicut ab![]() de eritque per praecedentem, sicut ac
de eritque per praecedentem, sicut ac![]() dg sic ab
dg sic ab![]() de et sicut bc
de et sicut bc![]() eg // fuit autem per26 hypothesim sicut ab
eg // fuit autem per26 hypothesim sicut ab![]() de sic ac
de sic ac![]() df.
25
Igitur per 6am conceptionem, sicut ac
df.
25
Igitur per 6am conceptionem, sicut ac![]() df sic ac
df sic ac![]() dg quare per 2am conceptionem df et dg aequales, pars et totum quod est impossibile.
dg quare per 2am conceptionem df et dg aequales, pars et totum quod est impossibile.
11a
Magnitudines proportionales sunt et permutatim proportionales.
26
Sit a![]() b sicut c
b sicut c![]() d. Erit sicut a
d. Erit sicut a![]() c sic b
c sic b![]() d. Namque ratio a
d. Namque ratio a![]() c componitur ex rationibus a
c componitur ex rationibus a![]() b et b
b et b![]() c et ratio b
c et ratio b![]() d ex rationibus b
d ex rationibus b![]() c et c
c et c![]() d. Ergo per 7am conceptionem sicut a
d. Ergo per 7am conceptionem sicut a![]() c sic b
c sic b![]() d quod est propositum.
d quod est propositum.
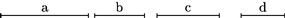
12a
Magnitudines proportionales sunt et coniunctim proportionales.
27
Sit ab![]() bc sicut de
bc sicut de![]() ef. Erit sicut ac
ef. Erit sicut ac![]() cb sic df
cb sic df![]() fe. Nam per praecedentem, erit permutatim, sicut ab
fe. Nam per praecedentem, erit permutatim, sicut ab![]() de sic bc
de sic bc![]() ef. Igitur per 9am erit ac
ef. Igitur per 9am erit ac![]() df sic bc
df sic bc![]() ef. Et rursus permutatim, sicut ac
ef. Et rursus permutatim, sicut ac![]() cb sic df
cb sic df![]() fe: quod est propositum.
fe: quod est propositum.

13a
28
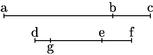
Magnitudines proportionales sunt quoque disiunctim proportionales. Sit ac![]() cb sicut df
cb sicut df![]() fe. Erit sicut ab
fe. Erit sicut ab![]() bc sic de
bc sic de![]() ef. Nam secus sit sicut ab
ef. Nam secus sit sicut ab![]() bc sic ge
bc sic ge![]() ef. Eritque per praecedentem, coniunctim sic ac
ef. Eritque per praecedentem, coniunctim sic ac![]() eb sic gf
eb sic gf![]() fe. Sed per hypothesim sicut ac
fe. Sed per hypothesim sicut ac![]() cb sic df
cb sic df![]() fe. Igitur per 6am conceptionem sicut df
fe. Igitur per 6am conceptionem sicut df![]() fe sic gf
fe sic gf![]() fe. Quare per pam conceptionem df, fg aequales, quod est impossibile.
fe. Quare per pam conceptionem df, fg aequales, quod est impossibile.
14a
29
Magnitudines proportionales sunt quoque eversim proportionales. Ut si sit ac![]() cb sicut df
cb sicut df![]() fe. Erit sicut ac
fe. Erit sicut ac![]() ab sic df
ab sic df![]() de. Quia tunc, per 11am erit sicut ac
de. Quia tunc, per 11am erit sicut ac![]() df sic cb
df sic cb![]() fe. Et ideo, per 10am sicut ac
fe. Et ideo, per 10am sicut ac![]() df sic ab
df sic ab![]() de. Et rursum per 11am sicut ac
de. Et rursum per 11am sicut ac![]() ab sic df
ab sic df ![]() de.
de.

15a
30
Magnitudines proportionales sunt et conversim proportionales. De rationibus nominatis, propositio manifesta est, quia per 5am, tales magnitudines sunt commensurabiles et ideo, per pam, sicut numerus ad numerum. Et numeri conversim servant idem nomen27.
31
Et ideo magnitudines conversim habent eiusdem nominis rationem, et per diffinitionem sunt proportionales. / Quando autem rationes non sunt nominatae, sit sicut ab![]() bc sic de
bc sic de![]() ef tunc dico quod cb
ef tunc dico quod cb![]() ba erit sicut fe
ba erit sicut fe![]() ed. Sit enim ratio ab
ed. Sit enim ratio ab![]() bg nominata, sicut de
bg nominata, sicut de![]() eh nominata. Eritque per diffinitionem similium rationum, ratio ab
eh nominata. Eritque per diffinitionem similium rationum, ratio ab![]() bc minor, quam ratio ab
bc minor, quam ratio ab![]() bg. Et ratio df
bg. Et ratio df![]() fe minor, quam ratio de
fe minor, quam ratio de![]() eh.
32
Sed conversim bg
eh.
32
Sed conversim bg![]() ba sicut eh
ba sicut eh![]() ed quia nominatae et de nominatis ostensum est maiorque ratio bc
ed quia nominatae et de nominatis ostensum est maiorque ratio bc![]() ba quam ratio bg
ba quam ratio bg![]() ga nominata. Et maior ratio28 ef
ga nominata. Et maior ratio28 ef![]() ed quam ratio eh
ed quam ratio eh![]() ed eiusdem nominis. Et similiter quacumque nominata ratione maior erit ratio cb
ed eiusdem nominis. Et similiter quacumque nominata ratione maior erit ratio cb![]() ba hac eadem maior ostendetur ratio ef
ba hac eadem maior ostendetur ratio ef![]() de.
33
Et quacumque minor: minor. Igitur per conversionem diffinitionis similium rationum, erit conversim cb
de.
33
Et quacumque minor: minor. Igitur per conversionem diffinitionis similium rationum, erit conversim cb![]() ba sicut ef
ba sicut ef![]() de quod est propositum.
de quod est propositum.
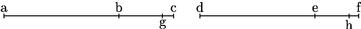
16a
Si fuerit ratio primae magnitudinis ad secundam, sicut ratio tertiae ad quartam. Ratio autem quintae ad secundam sicut ratio sextae ad quartam: ratio aggregatae ex prima et quinta ad secundam erit sicut ratio sextae et tertiae ad quartam.
34
Hoc est sit ab![]() c sicut de
c sicut de![]() f. Item sit bg
f. Item sit bg![]() c sicut eh
c sicut eh![]() f. Tunc dico quod totum ag
f. Tunc dico quod totum ag![]() c erit sicut totum dh
c erit sicut totum dh![]() f. Nam per praecedentem erit conversim c
f. Nam per praecedentem erit conversim c![]() bg sicut f
bg sicut f![]() eh. Igitur per 7am conceptionem erit ab
eh. Igitur per 7am conceptionem erit ab![]() bg sicut de
bg sicut de![]() eh. [A:15r] Et coniunctim per 12am erit ag
eh. [A:15r] Et coniunctim per 12am erit ag![]() gb sicut dh
gb sicut dh![]() he. Rursus ergo per dictam conceptionem fiet sicut ag
he. Rursus ergo per dictam conceptionem fiet sicut ag![]() c sicut dh
c sicut dh![]() f. Quod erat demonstrandum.
f. Quod erat demonstrandum.
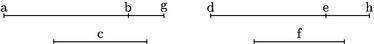
6 februarii