XI. Datum conum plano sic secare, ut sectio sit hyperbole similis, et aequalis datae hyperbola.

Sit datus conus abg; dataque hyperbole de; etc. sicut in praecedenti oportet iam conum abg plano sic secare, ut sectio sit hyperbole similis, et aequalis datae hyperbolae de. Secetur per praecedentem conus abg plano, ut sectio sit ml similis ipsi de hyperbolae. Atque si transversa ln transversae ez, et recta lx rectae eh fuerint aequales. Iam per corollarium 3. huius, hyperbolae ml similis, et aequalis erit hyperbolae de. [S:178] Et factum est quod faciendum proponitur.

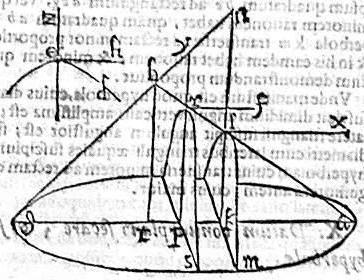
Si autem transversa ez minor, maiorve fuerit transversa ln tunc sicut est ln ad ez, sic sit bn, ad by (producta, vel abscissa bn), et ipsi bt aequidistans ducatur yrp; et ad rectos ipsi ag excitetur ps; et extenso plano, in quo rp, ps, secante conum sit sectio sr. Dico itaque quod sr hyperbole est similis, et aequalis hyperbolae de. Sit enim sicut quadratum bt ad rectangulum atg, sic yr ad rf. Eritque per 12. 1. conicorum, sectio br hyperbole, cuius transversa ry, et recta rf; et sicut ze ad eh, sic ry ad rf: quoniam est viraque sicut quadratum bt ad rectangulum atg. Et quoniam propter similitudinem triangulorum bln, bry, sicut est bn ad by, sic est ln ad ry. Fuitque ln ad ez, sicut bn ad by, idcirco ln eamdem habet rationem ad ez, et ry. Aequales ergo sunt ez, ry. Sed ze ad eh, sicut ry ad rf. Igitur et ipsae eh, rf aequales, itaque hyperbolarum de, sr transversae ez, ry aequales; et rectae eh, rf aequales. Igitur per corollarium 3. huius, hyperbole de, sr sunt inter se similes, et aequales. Datum ergo conum abg, plano sic secavimus ut sectio iam sr hyperbole. Sit similis, et aequalis datae hyperbolae de. Quod iam proponitur faciendum.