PROPOSITIO XX.
Si sphaera, et cylindrus diametrum communem, et axem communem habeant, secentur autem parallelis quotlibet planis, quibus axis perpendiculariter instet: erunt sphaericae superficies cylindricis superficiebus inter eadem secantia plana interpositis singulae singulis aequales.
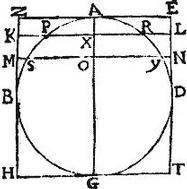
Circulo ABGD circumscribatur quadratum EZHT, sintque contactuum puncta A, B, G, D, et connectatur AG: item ducantur inter latera ZH, ET ipsisque EZ, HT paralleli, KL, MN ad placitum secantes axem, quidem AG apud X, O, peripheriam autem ABG apud P, R, S, Y: et circum AG diametrum immotam circumducatur, donec ad locum suum redat; parallelogrammum cylindrum, semicirculus vero sphaeram describet, eritque AG axis tam sphaerae, quam cylindri. Item EZ, HT diametri basium cylindri [S:64] sphaerae diametro aequales, et cylindrus sphaeram circumscribet: contingent namque cylindricae bases sphaericam superficiem in punctis AG; cylindrica quoque superficies sphaericam continget, eritque contactus circuli peripheria per punctum contactus B descripta. Ipsae quoque lineae KX, MO circumductae describent circulos parallelos secantes cylindrum, ipsa autem puncta PS describent circulorum peripherias, quae communes sectiones erunt dictorum circulorum secantium cylindrum, et sphaericae superficiei. Aio itaque quod sphaerica superficies interiacens circulis, quorum diametri ZE, KL, quae scilicet describitur ab arcu AP aequalis est cylindricae superficiei iisdem circulis interpositae, quae scilicet describitur a linea ZK. Item quod sphaerica superficies, quae inter circulos, quorum diametri KL, MN, quam scilicet describit arcus PS aequalis est cylindricae superficiei, quae inter eosdem circulos, quae scilicet a linea KM describitur. Item quod sphaerica superficies, quae inter circulos, quorum diametri MN, TH, quam scilicet describit arcus SBG aequalis est cylindricae superficiei, quae inter eosdem clauditur circulos, quam scilicet describit linea MH. Primum horum, et tertium patet per corollarium 15. praemissae. Cum cylindrus ZL habeat altitudinem aequalem ipsi AX, quae est axis segmenti sphaerici PAR, et basim circulum sphaerae maximum, atque etiam cum cylindrus MT habeat altitudinem OG, qui est axis segmenti sphaerici SGY, et basim circulum in sphaera maximum.
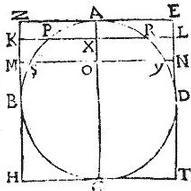
Secundum autem patet per 1. corollarium praecedentis. Cum cylindrus KN habeat altitudinem XO, qui est axis segmenti sphaerici SPRY, et basim circulum maximum sphaerae. Hoc idem ostendam de superficiebus sphaericis, ac cylindricis, quos intercipiant quaecunque duo plana parallela basibus cylindri, quibus scilicet axis cylindri rectus insistat: et hoc erat, quod demonstrandum proponebatur. Ostendam hoc idem aliter, cum per quartam huius. ex AG in peripheriam circuli ABG, quae basis est cylindri ZT, fiat superficies curva cylindri ZT; itemque ex AX in peripheriam eiusdem circuli fiat superficies curva cylindri ZL: propterea per 1. sex, et coniunctam proportionem, erit curva cylindri ZT superficies ad curvam cylindri ZL superficiem, sicut AG ad AX: sed per corollarium 17. praeteritae, sicut AG ad AX, sic sphaerae ABG superficies ad segmenti sphaerici PAR sphaericam superficiem. Igitur et sicut sphaerae ABG superficies ad segmenti PAR sphaericam superficiem, sic curva cylindri ZT superficies ad curvam cylindri ZL superficiem. Et permutatim sicut sphaerae ABG superficies ad curvam cylindri ZT superficiem, sic segmenti PAR sphaerica superficies ad curvam cylindri ZL superficiem; aequalis autem est per 11. huius, sphaerae ABG superficies curvae cylindri ZT superficiei: ergo et segmenti PAR sphaerica superficies aequalis est curvae cylindri ZL superficiei. Similiter ostendam quod segmenti SAY sphaerica superficies aequalis est curvae cylindri ZN superficiei: unde per consequentiam supererit sphaerica segmenti PY, quae zona est sphaerica ab arcu PS descripta aequalis curvae superficiei cylindri KN. Itemque sphaerici segmenti SGY superficies aequalis est curvae MT cylindri superficiei. Hoc idem ostendam quibuscumque planis cylindricae basi parallelis tam cylindrum, quam sphaeram cylindro circumscriptam secantibus, et hoc est, quod propositio nostra significat. Haec de superficiebus tornatilium, et sphaericorum segmentorum. Postulat ordo, ut iam de soliditate primum quidem tornatilis corporis, et exinde sphaerae disputemus.