PROPOSITIO XV.
Si sphaera plano secetur, segmenti utriuslibet sphaerica superficies aequalis est rectangulo, quod fit ex diametro sphaerae in peripheriam eius circuli, cuius diameter est axis segmenti.
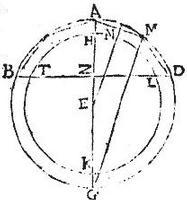
Sit circulus ABGD, cuius diameter AG, centrum E, secetur autem diameter AG recta BD ad angulos rectos in signo Z quocumque, et circumducto altero semicirculo ut puta ABG semel super axem AG stantem, describatur sphaera ABGD: unde in tali ambitu linea ZB describit circulum, qui secabit sphaeram in duo segmenta BAD, BGD. Aio itaque quod sphaerica superficies utriuslibet segmenti, ut puta segmenti BAD aequalis est ei, quod fit ex diametro AG in peripheriam circuli, cuius diameter est AZ, quem voco axem segmenti BAD. quae demonstratio similis est demonstrationi decimae. Nam si quod fit ex AG diametro in peripheriam circuli, cuius diameter AZ non est aequale superficiei sphaericae segmenti ABD, sit aequalis [S:58] superficiei sphaericae alicuius segmenti maiori, vel minori superficie segmenti BAD: et primum minori scilicet superficiei sphaericae segmenti THL abscissi per planum dicti circuli de sphaera HTKL, quam sphaerae ABG concentricam describit semicirculus HTK super diametrum HK, et secentur arcus AB, AD iterum, atque iterum donec per 13.12. arcuum chordae non contingant peripheriam THL, sitque una chordarum AM, et connectatur GM; eritque maius quod ex diametro AG in peripheriam circuli, cuius diameter AZ, quam id, quod ex GM, quae minor diametro in peripheriam circuli, cuius diameter AZ; sed quod ex diametro AG in peripheriam circuli, cuius diameter AZ per hypothesim aequale est superficiei segmenti sphaerici THL, quod autem ex GM in peripheriam circuli, cuius diameter AZ per praecedentem, aequale est superficiebus conicis descriptis a chordis arcuum, in quos secatur arcus AB maior: ergo superficies sphaerica segmenti THL, maior est, quam superficies conicae descriptae a chordis portionum arcus AB: superficies ergo inclusa maior includente, quod est impossibile. Vel sic quoniam quod fit ex AG diametro in peripheriam circuli, cuius diameter AZ maius est eo, quod ex GM in peripheriam eandem, et ideo maius superficiebus conicis descriptis per chordas portionum arcus AB, haeque superficies maiores sunt superficie sphaerica segmenti THL inclusa: ideo quod fit ex diametro AG in peripheriam circuli, cuius diameter AZ maius est superficie sphaerica segmenti THL: ergo non est ei aequalis, sicut supponebatur.

Sit deinde quod ex AG diametro in peripheriam circuli, cuius diameter AZ aequalis sphaericae superficiei maiori superficie sphaerica segmenti BAD; sed brevitatis causa sit suppositum segmentum THL. Aio quod id, quod ex HK diametro in peripheriam circuli, cuius diameter HZ non est aequale alicuius segmenti sphaericae superficiei maiori superficie segmenti THL sphaerici. Sit enim, si possibile est, aequale superficiei sphaericae segmenti BAD maiori superficie THL abscissi per planum circuli secantis sphaeram BD de sphaera ABGD, quam describit semicirculus ABG super diametrum AG, et secentur arcus AB, AD per 13.12. donec portionum chordae non contingant arcum THL; sitque ex chordis una AM, et connectatur GM, et ducatur ad AM perpendicularis EN, et quoniam AG dupla ipsius AE; ideo, et GM dupla ipsius EN, sed HK dupla ipsius HE minoris ipsa EN: minor ergo HK quam GM. Quare quod fit ex GM in peripheriam circuli, cuius diameter HZ maius est eo, quod fit ex HK in peripheriam circuli, cuius diameter HZ, sed quod fit ex GM in peripheriam circuli, cuius diameter AZ per praecedentem, aequale est superficiebus conicis descriptis a chordis arcuum, in quos secatur arcus AB: quod autem fit ex HK in peripheriam circuli, cuius diameter HZ per hypothesim aequale est superficiei sphaericae segmenti BAD: ergo superficies conicae descriptae a chordis portionum arcus AB maius sunt superficie sphaerica segmenti BAD. Superficies itaque inclusa maior includente, quod est impossibile: non est ergo, quod ex HK in peripheriam circuli, cuius diameter HZ aequale superficiei sphaericae segmenti alicuius maiori superficie sphaerica segmenti THL. Similiter ostendam quod id, quod ex AG in peripheriam circuli, cuius diameter AZ non est aequale alicuius segmenti sphaericae superficiei maiori superficie sphaerica segmenti BAD: fuitque ostensum, quod nec minori: omnino igitur id, quod fit ex AG in peripheriam circuli, cuius diameter AZ aequale est segmenti BAD sphaericae superficiei: quod erat demonstrandum. Suppo[S:59]suimus autem segmentum sphaericum BAD minus emisphaerio. Et similiter ostendi poterit quod id, quod fit ex AG in peripheriam circuli, cuius diameter GZ aequale est sphaericae superficiei segmenti BGD: vel si lubet pro linea BZ ducatur linea BE, et pro ZD linea ED secantes peripheriam circuli HTK apud puncta XO; et agatur demonstratio per segmenta sphaerica descripta per arcus BG, XK similes et per superficies conicas descriptas a chordis portionum arcus BG non tangentibus peripheriam XK: in secunda autem parte demonstrationis ducatur XO secans ipsam EZ apud P, eritque GZ axis segmenti BGD maior quam KP axis segmenti XKO, quod est necessarium in secunda parte demonstrationis: unde concludens eodem modo quo prius id, quod fit ex AG in peripheriam circuli, cuius diameter GZ esse maius omni superficie sphaerica segmenti descripti per arcum minorem ipso BG, et ei similem, et minus omni sphaerica superficie segmenti descripti per arcum maiorem ipso BG, et ei similem, et ideo aequalem esse sphaericae superficiei segmenti ab arcu BG descripti. Verum postquam ostenderis hoc de uno segmentorum sphaericorum, potest ex hoc idem facilius ostendi de reliquo, sic. Quoniam ostensum est quod id, quod fit ex AG in peripheriam circuli, cuius AZ est diameter aequum superficiei sphaericae segmenti BAD: ex hoc ego ostendam quod id, quod fit ex AG in peripheriam circuli, cuius diameter GZ aequum erit superficiei sphaericae segmenti BGD: nam per 10 huius. Superficies tota sphaerae ABG, quod est aggregatum ex superficiebus sphaericis duorum segmentorum BAD, BGD aequalis est ei, quod fit ex AG in peripheriam circuli ABG: sed peripheria circuli ABG per primum corollarium sextae aequalis est peripheriis circulorum, quorum diametri AZ, ZG, coniunctis: ergo aggregatum ex superficiebus sphaericis segmentorum BAD, BDG aequale est ei, quod fit ex AG in peripherias circulorum, quorum diametri AZ, ZG. Auferatur inde segmenti BAD sphaerica superficies: hinc vero quod fit ex AG in peripheriam circuli, cuius diameter AZ, quae, ut fuit ostensum, sunt aequalia; et supererit segmenti BDG superficies sphaerica aequalis ei, quod fit ex AG in peripheriam circuli, cuius diameter ZG: et hoc erat propositum.
COROLLARIUM I.
Manifestum est ergo quod superficies sphaerica segmenti sphaerici aequalis est ei, quod fit ex axe segmenti in peripheriam circuli maximi in sphaera; et ideo curvae superficiei cylindri, cuius basis est circulus maximus, sphaerae celsitudo vero, axis segmenti: hoc patet ex 2. corollario sextae.
COROLLARIUM II.
Item et circulus, cuius semidiameter media proportionalis est inter axem sphaerici segmenti ac sphaerae diametrum, aequalis est sphaericae superficiei ipsius segmenti; quod liquet ex quarto corollario primae: ex quo corollario facillime demonstrabitur sequens propositio decima sexta.