PROPOSITIO XXXII.
Adhuc idipsum aliter demonstrare.
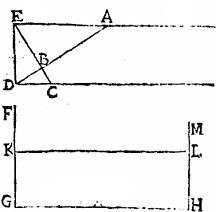
Sunto datae rectae AB, BG, quarum maior AB, describatur super AB diametrum circulus BGA intra quem per secundam quarti Euclidis coaptetur BG, quae producta occurrat ipsi AD tangenti circulum in puncto D: item EG secet ad rectos angulos diametrum AB in puncto Z, et super EG diametrum fiat semicirculus EHG rectus ad circulum BGA, hinc super semicirculum BGA erigatur hemicylindrus rectus; et in rectangulo, quod per axem cylindri describatur hemicirculus super AB, diametrum, qui semicirculus moveatur super planum circuli BGA semper rectus ad idem planum, moto scilicet diametro AB versus G, manente termino B immoto, sitque semicirculus iam motus TKB super diametro BT secante periferiam BGA in puncto L, quo quidem motu peripheria TKB describet in superficie cylindrica lineam quandam curvam; inde moveatur triangulum BDA super axem AB, quo motu punctum G circumferetur in peripheria EHG, et linea BD sic circulata describet conicam superficiem, et secabit lineam curvam in superficie cylindrica descriptam in puncto quodam, quod sit K, in quo peripheria TKB latus ipsum BD motum secabit: sit ergo BDA triangulum ad talem situm translatum ipsum BMA triangulariter; latere scilicet BM ipsam TKB peripheriam secante in puncto K, in ipsa cylindrica superficie. Et coniugatur KL recta; quae erit communis sectio plani TKB, et cylindricae superficiei, quoniam scilicet cylindrus rectus est, atque ideo planum ipsum TKB basi cylindricae rectum, aequidistat axi cylindrico. Quare KL eidem axi parallelus erit circulo BGA, et ideo rectae TB perpendicularis: praeterea communis sectio circuli TKB, et circuli EHG sit recta HN, quae per 19. undecimi Euclidis circulo BAG, et ideo rectae TB perpendicularis erit; et coniungantur TK, LH. Aio itaque, quod BL, BK ipsis BG, AB interiacent mediae proportionales. Quod sic demonstratur.
Nam per octavam sexti Elementorum Euclidis quadratum HN aequale est rectangulo EN, NG; et ideo adducta 34. tertii, rectangulo BN, NL: quo fit, ut angulus BHL sit rectus. Cum anguli BLK, BKT recti sint; erunt ob id triangula BHL, BLK, BKT similia; quandoquidem aequiangula. Unde sequitur, ut ipsae BH, BL, BK, BT sint continuo processu proportionales: verum BH aequalis ipsi BG, [S:19] quia sunt latera coni recti, cuius axis BZ, vertex autem B: item BT aequalis ipsi BA, per hypothesim. Igitur et BG, BL, BK, BA continuae proportionales erunt. Quod fuit demonstrandum. Est autem inventio Archytae Tarentini, ut refert Eudemus, et Eutocius:ingeniosa quidem, et tali viro digna speculatio, cuius praxis, et si difficilis sit, facillime tamen demonstratur.