F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  i  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de conoidibus et sphaeroidibus figuris Liber primus Propositio 20
<- App. -> <- = ->

PROPOSITIO XX.

Si conoides hyperbolicum plano secetur axi parallelo, vel per centrum hyperboles solidum describentis ducto: facta sectio erit hyperbole.

Esto solidum conoides descriptum ab hyperbola ABC; cuius axis BD, in quo extra producto, centrum sit Y (quod quidem centrum ab Archymede vertex coni comprehendentis solidum dicitur; qui conus describitur a non tangentibus proximis hyperbole) transversa diameter hyperbole sit XB, quae dicitur praecipua; diameter ex generatione sit ZF, parallela ipsi BX (in primo casu,) inter sectiones oppositas AB, et XZ interceptae, et (in secundo casu) singulae per medium secentur in centro Y: productaque (in utroque casu) diametro ZFG secante hyperbolem apud F erigatur super eam planum erectum super planum hyperboles ABC, et secans solidum. Aio quod sectio in solido [S:240] facta hyperbole erit, cuius axis ZFG; ducatur enim (in secundo casu) linea FE tangens hyperbolem apud F, et ductae occurrat BH tangens sectionem apud B verticem.

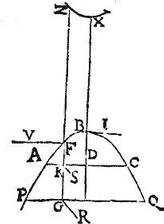
figura 1
Item per relicta puncta G, K in diametro FG ducantur tangenti FE lineae aequidistantes LGM, NKO, quae per 47. primi conicorum elementorum ordinatae erunt ad diametrum FG, et per medium sectae apud G, K puncta. Ducantur (in utroque casu per ipsa G, K puncta plana aequidistantia, et ad axem BD erecta; quorum communes sectiones cum hyperbola ABC sint lineae AC, PQ; eruntque per 17. huius, talium planorum sectiones in solido circuli quorum diametri AC, PQ: communes autem sectiones eorumdem planorum cum plano erecto per lineam FG sint lineae GR, KS; igitur sectio facta in solido per planum ductum per lineam FG ibit per puncta F, S, R, et circuli praedicti per puncta S, R. Demonstrandum est itaque quod peripheria FSR est hyperbole hoc modo.

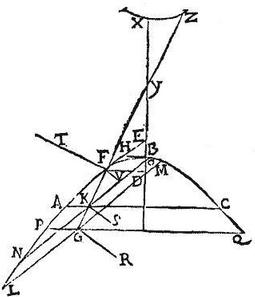
figura 2
In primo casu ducta BI recta diametro ipsius transversae BX, quia per 22. libri tertii Apollonii tam rectangulum ZGF ad rectangulum PGQ, seu ad quadratum GR, quam rectangulum ZKF ad rectangulum AKC, seu ad quadratum KS, eamdem rationem habent, quam transversa diameter XB ad rectam BI. Ergo permutando rectangulum ZGF ad rectangulum ZKF est sicut quadratum GR ad quadratum KS.

In secundo vero casu cum AC, PQ aequidistent ipsi BH tangenti; et LM, NO aequidistent ipsi FH tangenti: ideo per 17. tertii conicorum elementorum sicut quadratum BH ad quadratum HF, sic rectangulum PGQ, hoc est quadratum GR ad quadratum LG; et sic etiam rectangulum AK, KC, hoc est quadratum KS ad quadratum NK; et permutatim sicut quadratum GR ad quadratum KS, sic quadratum LG ad quadratum NK, sed ex 21. libri primi Apollonii rectangulum ZGF ad rectangulum ZKF est sicut quadratum LG ad quadratum NK: ergo quadratum GR ad quadratum KS est sicut rectangulum ZGF ad rectangulum ZKF, et ideo ex conversa eiusdem 21. libri primi Apollonii (in primo, et secundo casu) puncta F, S, R in hyperbola erunt, cuius transversa diameter ZF, quod erat ostendendum.

Inizio della pagina
 ->