|
PROPOSITIO IV.
Si ab extremo rectae ordinatae in parabola perpendicularis ad diametrum ducatur; erit sicut quadratum ductae ad quadratum, quod ex dimidio ordinatae, sic recta ad quam possunt ordinatae ad axem, ad rectam, ad quam possunt ordinatae ad diametrum.
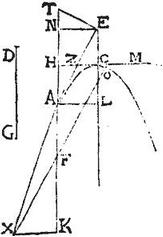
Sit parabola CAX; cuius axis ECL; recta ad quam possunt ordinatae ad axem CM. Ordinata ad axem LA; tangens parabolam in puncto A sit EA; diameter aequidistans axi TNHAFK; aequidistans tangenti, et perinde ordinata ad diametrum sit OFX; perpendicularis ad diametrum sit XK: item MC perpendicularis ad axem, et perinde tangens parabolam in vertice C producta secet tangentem apud Z, diametrum vero apud H: denique TE perpendicularis ad tangentem AE; et EN perpendicularis ad diametrum TA; recta vero, ad quam possunt ordinatae ad diametrum AK fit GD. Itaque demonstrandum erit, quod sicut est quadratum XK ad quadratum XF (quae est dimidia pars ipsius XO ad diametrum AK ordinatae) sic utique erit CM ad GD. Namque in primis quadratum LA est aequale rectangulo LCM, quandoquidem CM recta diameter est ordinatarum ad axem: ipsa autem GD recta diameter ordi[S:230]natarum ad diametrum AK dupla erit ipsius AT. Nam per 49. primi Conicorum elementorum sic est ZA ad AH, sive AT ad AE, hoc est sicut duplum AT ad duplum AE, sic iam recta diameter praedicta ad duplum AE.
 Eamdem igitur rationem habet duplum AT ad duplum AE; et recta diameter ad duplum AE; igitur recta diameter GD dupla est ipsius AT: haec quidem ex 52. primi Conicorum Elementorum ad inventionem talium diametrorum dicta sint. Itaque CM, AL, LC, continuae proportionales: aequalis autem AL ipsi EN. Igitur CM, EN, LC continuae proportionales erunt: item propter similitudinem triangulorum ipsae TN, NE, NA continuae proportionales sunt, ergo quadratum EN per 14. sexti elementorum aequale est tam rectangulo CM, LC, quam rectangulo TN, NA (quando quadratum LA aequum est rectangulo CM, LC) et ideo per 16. sexti elementorum sicut LC ad NA, sic TN ad CM. Sed per 35. primi elementorum Conicorum LC dimidia pars est ipsius LE. Hoc est ipsius NA. Igitur TN semissis est ipsius CM, sed AT (ut ostensum est) dimidium ipsius GD; ergo permutatim NT ad TA, sicut iam CM ad GD; verum NT ad TA est sicut quadratum ET ad quadratum TA (nam propter similitudinem triangulorum ETN, et ETA lineae NT, TE, TA sunt continuae proportionales.) Postea cum propter similitudinem triangulorum KXF, ETA sit sicut quadratum ET ad quadratum TA, sic quadratum KX ad quadratum XF (quoniam scilicet latera proportionalia.) Erit et sicut quadratum KX ad quadratum XF, sic CM ad GD. Quod fuit demonstrandum, quae tamen demonstratio ab Archimede tamquam manifesta, et in Conicis tradita, omissa est.
Eamdem igitur rationem habet duplum AT ad duplum AE; et recta diameter ad duplum AE; igitur recta diameter GD dupla est ipsius AT: haec quidem ex 52. primi Conicorum Elementorum ad inventionem talium diametrorum dicta sint. Itaque CM, AL, LC, continuae proportionales: aequalis autem AL ipsi EN. Igitur CM, EN, LC continuae proportionales erunt: item propter similitudinem triangulorum ipsae TN, NE, NA continuae proportionales sunt, ergo quadratum EN per 14. sexti elementorum aequale est tam rectangulo CM, LC, quam rectangulo TN, NA (quando quadratum LA aequum est rectangulo CM, LC) et ideo per 16. sexti elementorum sicut LC ad NA, sic TN ad CM. Sed per 35. primi elementorum Conicorum LC dimidia pars est ipsius LE. Hoc est ipsius NA. Igitur TN semissis est ipsius CM, sed AT (ut ostensum est) dimidium ipsius GD; ergo permutatim NT ad TA, sicut iam CM ad GD; verum NT ad TA est sicut quadratum ET ad quadratum TA (nam propter similitudinem triangulorum ETN, et ETA lineae NT, TE, TA sunt continuae proportionales.) Postea cum propter similitudinem triangulorum KXF, ETA sit sicut quadratum ET ad quadratum TA, sic quadratum KX ad quadratum XF (quoniam scilicet latera proportionalia.) Erit et sicut quadratum KX ad quadratum XF, sic CM ad GD. Quod fuit demonstrandum, quae tamen demonstratio ab Archimede tamquam manifesta, et in Conicis tradita, omissa est.
|
