Scrivere con LaTeX
(corso di LaTeX in $N^2$% WIDTH=26 HEIGHT=16 puntate)

Riccardo Murri
<murri@phc.unipi.it>

Continuiamo la panoramica su come comporre formule con LaTeX: questa volta vediamo come produrre nuovi simboli a partire da quelli noti a LaTeX, e come definire nuovi comandi.

Quasi tutti i comandi presentati qui di seguito richiedono le estensioni matematiche AMS, che si attivano aggiungendo la riga 

\usepackage{amsmath}
nel preambolo del documento.


Cambiare stile nelle formule

L'uso dei diversi stili di caratteri nelle formule serve in genere a produrre varianti grafiche di lettere o simboli, per aumentare il numero di segni disponibili, piuttosto che per marcare la diversa significatività di un brano, come avviene nel testo ordinario; dunque i comandi che andiamo ad esaminare si applicheranno raramente a formule più lunghe di un piccolo gruppo di caratteri.

Abbiamo già visto (cfr. Linux & C. n. 2) come i comandi per cambiare lo stile dei caratteri abbiano un funzionamento diverso nel modo matematico: permettono di inserire testo ordinario in una formula, secondo lo stile indicato. Come si fa allora per inserire una ``A'' in carattere grassetto in una formula? Si usano comandi simili, sostituendo però il prefisso \math al prefisso \text: la figura 1 riporta un elenco. Ognuno di questi comandi accetta un solo argomento: la formula da rendere nello stile corrispondente.


Figure: I vari stili disponibili per i caratteri matematici. Negli ultimi due è possibile produrre solo lettere maiuscole.

\begin{figure} \begin{center} \begin{tabular}{\vert l\vert r\vert} \hline \v... ...Z}' &\(\mathbb{ABC \dots Z}\)\\ \hline \end{tabular} \end{center}\end{figure}% WIDTH=551 HEIGHT=136

Alcune precauzioni d'uso:

Tutti i simboli sono disponibili in tutti gli stili? Provate ad ottenere lettere greche con \mathbf, \mathsf o \mathtt. Il simbolo ``<'' si può avere in \mathsf? Ed in \mathbf? E il simbolo di ``maggiore-o-uguale''?


Simboli in grassetto

Dato che le lettere greche e molti simboli non alfabetici non si possono ottenere con \mathbf, LaTeX definisce i comandi \boldsymbol e \pmb per raggiungere questi effetti. La figura 2 mostra le differenze tra i due ed il normale carattere matematico.
Figure 2: Differenze tra il normale carattere matematico, e le varie specie di grassetto disponibili in LaTeX.

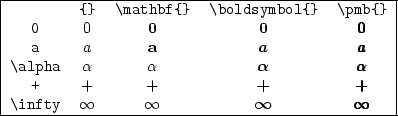
\begin{figure} \begin{center} \begin{tabular}{\vert ccccc\vert} \hline &\ver... ...ol{\infty}\)&\(\pmb{\infty}\)\\ \hline \end{tabular} \end{center}\end{figure}% WIDTH=398 HEIGHT=116

\boldsymbol accetta un solo argomento, che deve essere una lettera, una cifra od un comando che produce un simbolo (ad esempio, \pi o \cap), e disegna una versione in grassetto del simbolo, cifra o lettera indicato.

\pmb ha la stessa sintassi di \boldsymbol, ma effetti grafici lievemente differenti.


Accenti matematici

TeX utilizza lo stesso sistema per comporre le lettere accentate del testo ordinario (come à, é, ï) ed i simboli che si usano nella scrittura matematica per distinguere differenti specie di variabili (segni di vettore, tilde, ecc.); questi ultimi prendono perciò il nome di ``accenti matematici'' nel gergo TeXnico.
Figure 3: I comandi che producono accenti in LaTeX. Gli ultimi tre accenti sono usati solo nel modo matematico.

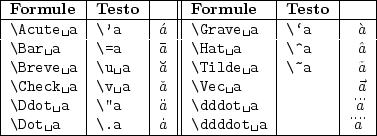
\begin{figure} \begin{center} \begin{tabular}{\vert l\vert l\vert r\vert\vert ... ...b*'\ddddot a'& &\(\ddddot a\)\\ \hline \end{tabular} \end{center}\end{figure}% WIDTH=377 HEIGHT=136

La figura 3 riporta i comandi disponibili in LaTeX per produrre accenti (matematici e non). Esistono dunque due tipi di questi comandi, uno da utilizzare solo nel modo matematico per comporre formule, e l'altro da usare solo nel testo ordinario; TeX riporta un errore se usate un comando nel contesto sbagliato.

Tutti i comandi che producono accenti sono implementati in modo da sovrapporre un segno all'argomento: un po' come se in una macchina da scrivere battessimo un apostrofo, poi tornassimo indietro e scrivessimo una ``a'' per ottenere ``á''. Alcune versioni di xdvi non gestiscono bene queste sovrapposizioni e non riescono a mostrare le lettere accentate: è questo il senso del messaggio ``Overstrike characters may look incorrect''; tuttavia, la stampa sarà sempre corretta.

Questi comandi permettono di scrivere lettere accentate anche in un file di testo contenente solo i caratteri ASCII, o avendo a disposizione una tastiera USA. In genere è però più comodo scrivere le lettere accentate del testo direttamente nel file: per questo basta aggiungere la riga 

\usepackage[latin1]{inputenc}
al preambolo del documento.

Notate che si possono omettere le parentesi graffe quando l'argomento di un comando è costituito di una sola lettera: possiamo scrivere \'e invece di \'{e} e \Tilde a invece di \Tilde{a}, ma i due modi sono del tutto equivalenti. Cosa produce il codice \Tilde{MA}? Ovvero, cosa si ottiene cercando di porre un accento sopra un argomento più largo di una lettera?


Figure: I comandi per ornare formule più larghe di una lettera.

\begin{figure} \begin{center} \begin{tabular}{\vert l\vert r\vert} \hline \e... ...{xyz}\), \(\underbrace{xyz}\)\\ \hline \end{tabular} \end{center}\end{figure}% WIDTH=524 HEIGHT=182

LaTeX definisce dei comandi speciali per ornare formule più larghe di una lettera: la figura 4 ne riporta l'elenco completo. Tutti questi comandi accettano argomenti di lunghezza arbitraria, ad eccezione di \widehat e \widetilde che possono allargarsi al più su 3 lettere (provare per credere).

I comandi \underbrace e \overbrace permettono di disporre delle scritte sopra o sotto il segno che appongono su una formula, tramite la consueta notazione degli esponenti e deponenti: un esponente ^{...} dopo \overbrace indicherà il testo da collocare sopra la parentesi graffa, così come un deponente _{...} dopo \underbrace specifica quello da porre sotto la parentesi graffa. Esaminiamo gli esempi di figura 5: siccome \underbrace e \overbrace funzionano solo in modo matematico, sia l'argomento di questi comandi, che l'eventuale esponente o deponente vengono interpretati come formule. Nel primo esempio di figura 5, si usano il comando \text per inserire del testo (che a sua volta contiene una formula!).
Figure 5: Esempi di testo a completare l'ornamento di una formula.

\begin{figure} \begin{center} \begin{tabular}{\vert l\vert m{0.15\textwidth}\v... ...{T_1T_2\dots T_n}_{=S^{-1}}\)\\ \hline \end{tabular} \end{center}\end{figure}% WIDTH=517 HEIGHT=116


Accenti doppi

Gli accenti di figura 3 si possono raddoppiare: ad esempio, \Bar{\Bar A} (Quiz: perché il secondo accento è tra parentesi graffe?) produce una lettera ``A'' sormontata da una doppia riga.

Questa operazione di raddoppiamento è complicata e può rallentare TeX se eseguita troppo spesso; LaTeX definisce perciò il comando \accentedsymbol, che permette di costruire comandi che producono combinazioni complesse di accenti. \accentedsymbol accetta due argomenti: il primo è il nome di un comando da definire (completo di \) ed il secondo è il codice LaTeX per produrre il simbolo accentato che vogliamo: 

\accentedsymbol{\Ttildetilde}{\Tilde{\Tilde T}}
crea il comando \Ttildetilde che disegna una ``T'' sormontata da una doppia tilde. Sono possibili anche combinazioni molto più orribili. I manuali di LaTeX consigliano di definire nel preambolo del documento un comando per ogni simbolo accentato di cui ci sarà bisogno in seguito.

Attenzione! \accentedsymbol si può usare solo nel preambolo di un documento; metterlo nel mezzo del testo provocherà un errore ``Undefined control sequence.''


Altri accenti matematici

LaTeX mette a disposizione anche un comando per approssimare i tipi di accenti non disponibili coi comandi standard; il comando \overset accetta due argomenti, il primo dei quali è un simbolo che verrà collocato sopra il testo indicato nel secondo argomento. Ad esempio, \overset{*}{X} scriverà un asterisco sopra la lettera ``X''. Esiste anche un comando \underset che pone il simbolo nel primo argomento sotto il testo. Attenzione! I comandi \overset e \underset si possono usare solo nel modo matematico.

Come si può mettere un accento sopra le lettere ``i'' o ``j''? Provando, noterete che il puntino sta pressappoco all'altezza dell'accento, e dà un risultato esteticamente poco piacevole; TeX definisce \imath e \jmath da usare in combinazione con i comandi che producono accenti per ottenere ``i'' e ``j'' correttamente accentate: \Grave\imath renderà appunto una lettera ``ì''. Come dice il nome, questi due comandi funzionano solo nel modo matematico.

Il comando \not permette di sovrapporre una barra ``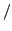\(\slash\)% WIDTH=12 HEIGHT=31 '' al simbolo che lo segue; si possono creare così i segni ``diverso-da'', ``non-equivalente'', ecc. in una formula. Sebbene \not non sia propriamente un accento, il principio di funzionamento di questo comando è lo stesso di \Acute,, \Bar, ecc.


Definire nuovi comandi

Ormai vi sarete accorti che la scrittura in TeX tende a volte ad essere un po' verbosa, e che le stesse sequenze di comandi ricorrono più volte nel corso di uno stesso documento; per fortuna e per comodità, LaTeX permette ai suoi utenti di definire nuovi comandi. Il comando per fare ciò si chiama, appunto, \newcommand, ed ha diverse forme sintattiche.


Comandi senza argomenti

Il più semplice utilizzo di \newcommand sta nel definire abbreviazioni per parti di testo frequentemente ricorrenti; in questa sua forma più semplice, \newcommand prende due argomenti, il primo dei quali è il nome del comando da definire (completo di \) ed il secondo è una stringa che dovrà essergli sostituita; questa stringa si dice ``espansione'' del comando. Ad esempio, 

\newcommand{\gnu}{GNU's Not \textsc{Unix}}
definisce un nuovo comando \gnu il cui effetto sarà di produrre il testo ``GNU's Not UNIX''.

Non si possono definire con \newcommand dei comandi che siano già definiti; per via dei meccanismi interni di LaTeX, non si possono definire neanche comandi il cui nome comincia con ``\end''. (Per esempio, \endymione)

Come si vede dall'esempio qui sopra, l'espansione di un comando può contenere altri comandi, ma non il comando che si sta definendo: 

\newcommand{\gnu}{\gnu's Not \textsc{Unix}}
è una definizione circolare, e provoca un errore ``TeX capacity exceeded''. Il 99% delle volte questi errori sono causati da definizioni circolari, e non da una reale necessità di aumentare la memoria a disposizione di TeX. Attenzione! TeX sostituisce l'espansione di un comando quando lo incontra nel testo, e non al momento della definizione: se quindi definite il comando \gnu come sopra, TeX riporterà errore alla prima occorrenza di questo comando nel documento.

Per via della sintassi usata da TeX per individuare gli argomenti da passare ai comandi, tutti gli spazi che seguono un comando senza argomenti sono ignorati. Si può usare il comando \ (barra inversa-spazio) per inserire uno spazio dopo un comando.

Ancora, si può usare \newcommand per definire notazioni di uso comune: ad esempio, 

\newcommand{\R}{\mathbb{R}}
permette di usare \R per produrre il simbolo del campo dei numeri reali. L'espansione di questo comando contiene \mathbb che funziona solo nel modo matematico, perciò anche il nuovo comando \R funzionerà solo nel modo matematico: dovremo perciò scrivere: 
 il campo \( \R \) dei numeri reali,
e non 
 il campo \R \ dei numeri reali.
(Perché \R è seguito da barra inversa-spazio?)

LaTeX permette di aggirare questa limitazione: il comando \ensuremath compila in modo matematico il suo unico argomento, indipendentemente dal contesto in cui occorre. Adattando l'esempio precedente, 

\newcommand{\R}{\ensuremath{\mathbb{R}}}
definisce un comando \R che si può usare indifferentemente e con gli stessi effetti sia in mezzo ad un paragrafo di testo che ad una formula.

Insomma, i comandi definiti con \newcommand possono funzionare sia nel modo di testo (LR mode) che in quello matematico: tutto dipende dalla loro espansione.


Comandi con argomenti

È anche possibile definire nuovi comandi che accettano argomenti (fino a 9; questo è un limite di TeX), usando una forma alternativa di \newcommand:

\newcommand{comando}[numero degli argomenti]{espansione}
Se le combinazioni di caratteri #1, ..., #9 compaiono nell'espansione, verranno sostituite con il primo, il secondo, ..., il nono argomento. (Quiz: perché allora non ci possono essere più di nove argomenti in un comando?)

Un esempio chiarirà meglio le cose: 

\newcommand{\lasecondachehaidetto}[2]{\emph{#2}}
definisce un comando che stampa il suo secondo argomento enfatizzato ed ignora il primo; più in dettaglio, se inseriamo \lasecondachehaidetto{perché}{quando} nel mezzo di un documento, durante la compilazione del documento accade che:
1.
TeX lo sostituisce con la sua espansione \emph{#2};
2.
scorre questa alla ricerca delle combinazioni di caratteri #1 e #2;
3.
trova #2 e la sostituisce con il secondo argomento ``quando''.
Alla fine è come se avessimo scritto \emph{quando} nel documento. Cosa succede se al posto di #2 si scrive #1? E se ci mettiamo #3?

Un esempio più complicato: 

\newcommand{\D}[2]{\frac{\partial #2}{\partial #1}}
Cosa fa questo comando? Quanti argomenti accetta? Si può usare in modo testo? (cfr. figura 6)


Comandi con argomenti facoltativi

Un'ultima forma di \newcommand consente di definire un comando il cui primo argomento è opzionale:

\newcommand{comando}[numero degli argomenti][valore del primo argomento]{espansione}
Il primo argomento dovrà essere posto fra parentesi quadre, altrimenti il valore indicato nella definizione verrà sostituito a #1 nell'espansione. Non è possibile rendere facoltativi altri argomenti oltre il primo.

Per esempio, definiamo un comando \H con un solo argomento (facoltativo) che produce una lettera ``H'' seguita dal suo primo argomento in esponente; se il primo argomento non è specificato, dovrà mettere in esponente un asterisco: 

\newcommand{\H}[1][*]{\ensuremath{H^{#1}}}
Provate: cosa produce \(\H(X)\)? e \(\H[n](X)\)? e con \(\H{4}(X)\) cosa si ottiene? Come estendereste il comando \D definito prima per scrivere derivate di ordine superiore?


Ridefinire i comandi

Non si può usare \newcommand per definire un comando esistente, ma occorre usare la variante \renewcommand; questa ha esattamente la stessa sintassi di \newcommand, ma permette di costruire solo comandi già definiti.

Ad esempio, supponiamo di decidere che vogliamo rappresentare i vettori in stile grassetto, e non con la consueta freccettina; la via più breve per farlo è di ridefinire il comando \Vec in modo che stampi il suo argomento in grassetto: 

\renewcommand{\Vec}[1]{\mathbf{#1}}

Attenzione! TeX sostituisce ad un comando la sua espansione quando questo comando occorre nel documento, quindi anche con \renewcommand bisogna prestare attenzione alle definizioni circolari: 

\renewcommand{\Vec}[1]{\Vec{\boldsymbol{#1}}}
non produce un comando che pone una freccettina sopra un simbolo in stile grassetto, ma genera invece un errore: TeX non può distinguere \Vec nel secondo argomento da quello nel primo.

Ancora, questo distrugge la vecchia definizione di \Vec, e non è più possibile sovrapporre la freccettina ad un carattere!

Analizziamo meglio questa situazione: \Vec è un comando la cui interpretazione è ``metti una freccina sopra il simbolo che segue'', e non ``il simbolo che segue rappresenta un vettore''; \Vec fornisce quindi una indicazione tipografica. Viceversa, il comando \title fornisce una indicazione sulla categoria logica del suo argomento: 

\title{Il lavoro mi perseguita, ma io sono più veloce}
implica che il testo ``Il lavoro mi perseguita, ma io sono più veloce'' è il titolo del documento, quindi deve ricevere un trattamento tipografico particolare (per esempio, sarà stampato in grassetto e con un carattere grande, oppure in maiuscoletto, ecc.); il fatto di aver marcato quel testo come ``titolo'' permette anche ad esempio di riprenderlo nell'intestazione di ogni pagina, cosa che non sarebbe stata possibile se lo avessimo semplicemente indicato a TeX di impaginarlo come ``grassetto 18pt.''

LaTeX non può fornire comandi per marcare la categoria logica di ogni possibile brano di testo, ma ciascuno può definire i propri tramite \newcommand e \renewcommand: l'espansione di questi comandi indicherà il trattamento tipografico da riservare a queste particolari parti di testo.

Il modo consigliato nei manuali di LaTeX per gestire queste situazioni consiste nel definire comandi che indichino la categoria o la funzione logica che un simbolo ha, e usare questi comandi per produrre gli effetti tipografici desiderati.

Un esempio per chiarire meglio: l'accento \Bar è usato in matematica per svariate notazioni; se in un documento usiamo questo comando per indicare due costrutti diversi (``...dal contesto risulterà chiaro di cosa si sta parlando ...''), saremo in difficoltà non appena dovremo usarle entrambe in una formula (per la legge di Murphy, questo capiterà quasi certamente). Se invece definiamo: 

\newcommand{\cl}[1]{\Bar{#1}} % chiusura toplogica
\newcommand{\grad}[1]{\Bar{#1}} % parità dell'elemento
\newcommand{\ext}[1]{\Bar{#1}} % estensione
potremo scrivere tranquillamente \cl{A}, \grad{a}, \ext{f} e cambiare ad esempio 
\newcommand{\grad}[1]{|#1|}
se dobbiamo applicare sia \grad che \ext ad un elemento; in questo modo è possibile cambiare consistentemente e facilmente la notazione in tutto un documento.

Un altro esempio: il corsivo è usato normalmente nel testo per enfatizzare parole, oppure, invece delle virgolette, per riportare brevi citazioni o parole straniere. Il comando \emph ha in effetti una interpretazione come ``enfatizza il testo in argomento'', ma non esistono comandi specifici per gli altri due scopi. Potremmo perciò definire: 

\newcommand{\citazione}[1]{\emph{#1}}
\newcommand{\parolastraniera}[1]{\emph{#1}}
e poi permetterci di cambiare idea e decidere che vogliamo mettere le citazioni tra virgolette; basterà allora cambiare una sola riga del documento: 
\newcommand{\citazione}[1]{``#1''}


Figure 6: Esempi di definizione di nuovi comandi.

\begin{tabular}{\vert m{0.5\textwidth}\vert>{\Large }m{0.33\textwidth}\vert} \h... ...vettori \(\vec a\), \(\vec b\)\ldots \end{minipage} \\ \hline \end{tabular}% WIDTH=580 HEIGHT=673


Saluti e baci

Basta ora con le formule matematiche, e vedremo un'altra volta come trattare alcune raffinatezze tipografiche. La prossima puntata, però, tratterà nuovamente di come organizzare un testo comune in LaTeX. Ciao!

About this document ...

Scrivere con LaTeX
(corso di LaTeX in $N^2$% WIDTH=26 HEIGHT=16 puntate)

This document was generated using the LaTeX2HTML translator Version 98.2 beta6 (August 14th, 1998)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -white -address Riccardo Murri -split 0 -dir HTML -no_navigation -html_version 2.0 index.tex

The translation was initiated by Riccardo Murri on 1999-11-25

Riccardo Murri