Theorema XII

25 Transeuntibus per diaphanam sphaeram tribus parallelis radiis uno per centrum reliquis autem praeter centrum; qui per centrum in rectum transibit, at ei propior¹³² frangetur, ad ipsum tamen non perveniet. Reliquus quoque frangetur, sed alterum fractum nequaquam continget.

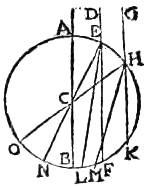
26 Esto perspicuus orbis¹³³ ab, cuius¹³⁴ centrum¹³⁵ c, per quem¹³⁶ transeant tres paralleli radii, ab per centrum, def autem et ghk [S:37] praeter centrum. Aio quod ab non frangitur sed de frangetur, et fractus ad diametrum ab non perveniet, sed ad signum l inter signa f, b¹³⁷; ipse quoque gh frangetur, fractus autem ad el non veniet, sed ad signum m inter ipsa k, l¹³⁸ signa. Quod enim ab non frangitur, [A:3v] per primum suppositum satis¹³⁹ patet. 27 Et¹⁴⁰ si el¹⁴¹ ipsam ab secaret vel ad b signum perveniret tunc¹⁴² ducta diametro en, angulus fen, qui a radio recto et perpendi[C:31r]culari comprehenditur ad angulum fractionis fel, aut duplus esset, aut minor, quam duplus, per 26^am 3ⁱⁱ¹⁴³, quod est falsum. ¹⁴⁴ Nam per corollarium 10^ae145, angulus inclinationis ad angulum fractionis est sicut 8 ad 3. Et si hm ad ipsam el perveniret tunc anguli inclinationum len, et mho, ducta ipsa ho, differrent in angulo qui consistit supra arcum no, aut minori. 28 Anguli autem fractionum fel et khm differrent in angulo, qui consistit supra arcum kf aut maiori¹⁴⁶, et ideo aequali ipsi¹⁴⁷ angulo in quo differunt anguli inclinationum propter aequalitatem arcuum kf, he, et¹⁴⁸ no, aut maiori¹⁴⁹. Sed anguli inclinationum sunt per 10^am150 fractionum angulis proportionales¹⁵¹ . Ergo in quatuor quantitatibus proportionalibus¹⁵² erit differentia maiorum¹⁵³ aequalis differentiae minorum aut minor, quod est impossibile. Oportet enim ut maior sit differentia maiorum quam¹⁵⁴ differentia minorum, quod per 19^am 5ⁱ¹⁵⁵ facile ostenditur. Destructis ergo oppositis, verum est propositum.