19

74 Icosahedrum construere et data sphaera comprehendere, et ostendere, quod ipsius icosahedri latus irrationale est, appellaturque minor.

Sit datae sphaerae diametros ab et ac quadrupla sit ipsius bc et excitata cd perpendiculari: ductisque ad db fiat primum ex semidiametro bd circulus efg intra quem claudatur [S:117] pentagonum efghk et decagonum lmnop. 75 A quibus punctis excitentur perpendiculares ad circulum lr, ms, nt, ou, pq. Quae singulae sint aequales ipsi bd. A punctis autem q, r, s, t, u singulis deducantur hypothemisae binae ad angulos pentagoni: quae sint qk, qh, vh, vg, tg, tf, sf, se, re, rk. Et quinque aliae transversae scilicet qr, rs, st, tv, vq connectant vertices harum perpendicularium et faciant pentagonum qrstv aequilaterum primo quae cum lateribus utriusque pentagoni facient decem triangula aequilatera. 76 Nam unaquaeque illarum hypothemisarum, per penultimam Primi, potest perpendicularem, quae est latus hexagoni circuli fg et latus decagoni.

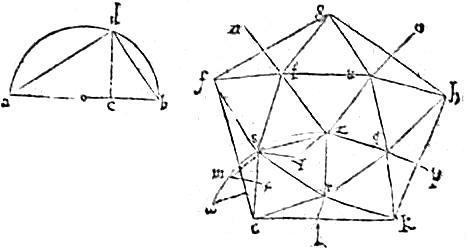
Et ideo, per 13^am huius, est aequalis lateri pentagoni. Item a centro circuli efg quod sit punctum x excitetur ipsi circulo perpendicularis xy quae sit ipsi bd aequalis, sicut aliae praedictae quinque perpendiculares. 77 Cui apponatur in rectum yz aequalis ipsi fn lateri scilicet decagoni: et eidem aequalis x. Tamque z quam connectatur cum quinque punctis pentagoni subiecti. Videlicet z cum punctis q, r, s, t, v. At vero , cum punctis e, f, g, h, k. Unde fient, quina utrinque, hoc est decem aliae triangula prioribus aequilatera. Quinque stilum concurrentia ad z punctum et totidem ad punctum. 78 Unaquaeque enim linearum poterit hexagoni et decagoni latus. Et ideo singulae erunt aequales ipsi ef ipsae enim mx, sy sunt semidiametri circulorum efg et qrs aequalium et latera hexagonica eorundem: sic completa sunt viginti triangula icosahedrum totum claudentia.

79 Et quoniam recta ab quincupla est ad ipsam bc ideo per 8^am et 7^am Sexti, quadratum ipsius ab quincuplum est ad quadratum ipsius bd sed per 11^am et 6^am huius quadratum z quincuplum est ad quadratum ipsius xy quae fuit aequalis ipsi bd igitur z aequalis est ipsi ab et quoniam xy media proportionalis est inter zy et zx et ideo inter ipsas zy et y. Ideo tam ys quam xm ipsi xy aequalis media proportionalis erit inter portiones diametri z. 80 Quare semicirculus descriptus super z diametro, ibit per ipsa sm puncta. Et semicirculus igitur super axe z stante semel revolutus describet sphaeram contingentem singulos icosahedri angulos. Et perinde ipsum icosahedrum circumscribentem. Cumque z sit ipsi ab aequalis, iam solidum ipsum a data [S:118] sphaera comprehendetur. 81 Et quoniam rationalis est bd quandoquidem in potentia commensurabilis est ipsi ab per hypothesim rationali, ideo et mx illi aequalis rationalis est: semidiameter scilicet circuli, cui pentagonum efg inscriptum est. Ergo per 14^am huius, et ipsum ef pentagoni latus, quod est et icosahedri latus, irrationalis est, quae minor factum est g quod faciendum, et ostensum quod ostendendum proponitur.