302 [A:92v] 48^a Eisdem existentibus: demonstrandum quod ductae lineae a tactu ad facta in axe puncta ex comparatione aequales faciunt angulos ad tangentem.

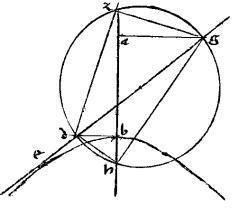
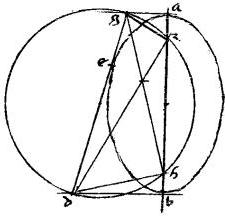
Supponantur⁴⁰⁹ eadem. // Et coniungantur ez eh. // Dico iam quod angulus gez aequalis est angulo deh. // 303 Nam, cum per 45^am huius rectus sit angulus dht et per praecedentem, rectus etiam angulus det. // Iam super diametro dt circulus ibit per e h puncta. // Et eadem ratione, super tg diametro circulus lineatus ibit per e z puncta. // Quam ob rem per 20^am tertii Euclidis angulus deh aequalis est angulo dth. // Itemque eidem dth angulo in hyperbole, vel eius contraposito gtz in ellipsi, aequalis est angulus gez. 304 // Igitur et angulus gez aequalis⁴¹⁰ angulo deh. // Quod est demonstrandum. ⁴¹¹