230 34^am Si hyperboles in una non tangentium relictum sit punctum: et ab ipso linea tangat sectionem: et per tactus ducatur aequidistans non tangenti; ducta per relictum punctum aequidistans alteri non tangentium; quae iam inter punctum ipsum et primam aequidistantem, a periferia sectionis per aequalia dividetur.

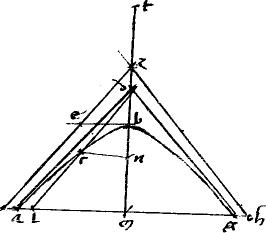
231 Sit hyperbole ab. // Non tangentes gde. // In quibus relictum punctum g. // Tangens sectionem gbe³⁵¹. // Punctum tactus b. [A:84v] // Ipsa zbh aequidistans ipsi gd. // Itemque gah aequidistans ipsi de. // Dico iam quod gh per medium secatur apud a periferiae punctum. // Ducantur enim ipsi dg aequidistans ipsa at ipsique de aequidistans ipsa bc. // Et, quoniam per 3^am secundi Conicorum, aequalis est gb ipsi be. 232 // Ideo per 2^am sexti Euclidis aequalis erit et gc ipsi cd. // Quare per primam eiusdem cgh aequale est bcd. // Sed per 12^am secundi Conicorum bcd aequale est agd. // Igitur agd aequale cgh. // Commune auferatur agc et supererit cdt et perinde ipsum agc aequale ahb. Quam ob rem, per primam sexti Euclidis ipsae bases ga ah aequales. // Quod fuit demonstrandum.